mọi người giúp mình với 
Cho mặt cầu (S): x2 + y2 +z2 =16 và hai điểm A, B thuộc mặt cầu. Diện tích của tam giác OAB có giá trị lớn nhất là :
A. 1 (đvdt)
B. 2 (đvdt)
C. 8 (đvdt)
D. 16 (đvdt)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
18 tháng 2 2017
Lời giải:
Ta có:
\((S): x^2+y^2+z^2-2x-2y-2z=0\)
\(\Leftrightarrow (x-1)^2+(y-1)^2+(z-1)^2=3\)
Do đó mặt cầu \((S)\) có tâm \(O=(1,1,1)\) và \(R=\sqrt{3}\)
Khi đó, dễ dàng nhận thấy \(A\in (S)\)
Ta có \(S_{OAB}=\frac{OA.OB.\sin \angle AOB}{2}\leq \frac{OA.OB.1}{2}=\frac{3}{2}\) vì \(\sin AOB\leq 1\)
Dấu bằng xảy ra khi \(\angle AOB=90^0\)
CM
17 tháng 7 2019
Đáp án là C
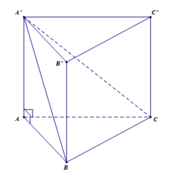
+) Ta có tam giác ABC là hình chiếu vuông góc của tam giác A'BC trên mặt phẳn (ABC)
+) Gọi φ là góc giữa (A'BC) và (ABC).
Ta có :
11 tháng 7 2016
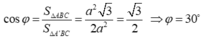
1) \(A=\frac{x^2+2x+9}{-2y-y^2+3}=\frac{\left(x^2+2x+1\right)+\left(2y^2+4y+2\right)+2\left(-y^2-2y+3\right)}{-y^2-2y+3}=\frac{\left(x+1\right)^2+2\left(y+1\right)^2}{-y^2-2y+3}+2\ge2\)Vậy Min A = 2 \(\Leftrightarrow\hept{\begin{cases}x=-1\\y=-1\end{cases}}\)
CM
29 tháng 3 2018
Đáp án là C
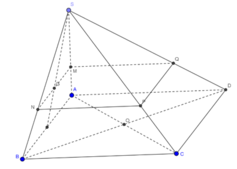
Cách 1. Ta có mặt phẳng (P) đi qua trọng tâm của tam giác SAB cắt các cạnh của khối chóp lần lượt tại M, N, P, Q. Với MN//AB, NP//BC, PQ//CD, QM//AD.
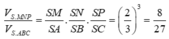
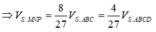
Tương tự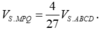 
Nên 
Đặt AB = x.
Ta có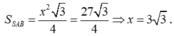 
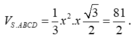
Từ đó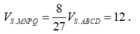 
Cách 2. Do hai khối chóp S.MNPQ, S.ABCD đồng dạng với nhau theo tỉ số k = 2 3 nên tỉ lệ thể tích là
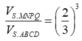
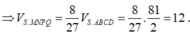
Giải:
Mặt cầu \((S)\) có bán kính là \(R=\sqrt{16}=4=OA=OB\)
Do đó diện tích tam giác \(OAB\) là:
\(S_{OAB}=\frac{OA.OB.\sin AOB}{2}\leq \frac{OA.OB}{2}=8(\text{đvdt})\)
Dấu bằng xảy ra khi \(\sin AOB=1\Leftrightarrow \angle AOB=90^0\)
Đáp án C.
B.2(đvdt)