Cho hàm số y = f(x) = \(\frac{48-3x}{15-x}\) với x là số nguyên , x khác 15.
Giá trị lớn nhất của hàm số đạt được khi x đạt giá trị .... (giải chi tiết nha)
(Mấy bạn cố gắng giúp mk , mai mk thi rùi )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

000000000000000000000000000255555555555555555555555555555555555555555555555555555

\(f\left(x\right)=\frac{48-3x}{15-x}=\frac{3+45-3x}{15-x}=\frac{3+3\left(15-x\right)}{15-x}=3+\frac{3}{15-x}\)
Để \(f\left(x\right)=3+\frac{3}{15-x}\) đạt GTLN <=> \(\frac{3}{15-x}\) đạt GTLN
=> 15 - x là số nguyên dương nhỏ nhất => 15 - x = 1 => x = 14
\(\Rightarrow f\left(x\right)_{min}=\frac{48-3.14}{15-14}=\frac{6}{1}=6\)
Vậy GTNN của f(x) là 6 tại x = 14

Cho \(x=\frac{1}{4}\Rightarrow2.f\left(\frac{1}{\frac{1}{4}}\right)=\left(\frac{1}{4}\right)^2\)
\(\Rightarrow2f\left(4\right)=\frac{1}{16}\Rightarrow f\left(4\right)=\frac{1}{32}\)

Vẽ hình:
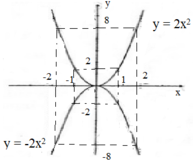
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.

Vẽ hình:
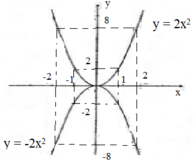
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
Bước 1.Đầu tiên phân tích cái tử thành hai số hạng trong đó một số hạng phải có nhân tử giống cái mẫu: 3.(15-x)+3--
bước 2 chia tử cho mẫu: \(y=\frac{3\left(15-x\right)+3}{15-x}=3+\frac{3}{15-x}\)
Bản chất số "3" là thương của cái thừa số phân tích trong bước 1 (3.15-3)/(15-3)=3. "tự nhiên (trừ 3)=>? 3 lấy ở đâu.
Bước 3. giờ đơn giản rồi f(x) là tổng hai số hạng (1 hằng số)=> chỉ xét số hạng chứa x : g(x) =3/(15-x)
bước 4. cần f(x) lớn nhất--> g(x) phải lớn nhất--> g(x) trước hết g(x) phải >0. --> x phải nhỏ hơn 15
bước 5 ; để phân số lớn nhất --> mẫu số phải nhỏ nhất--> 15-x phải nhỏ nhất là một số dương===> 15-x=1=> x=14
Kết luận: f(x)=3+3/(15-14)=6
đầu tiên bạn lấy f(x) ban đầu trừ đi 3 sẽ còn lại là 3/15-x
=> f(x) Max <=> 3/15-x lớn nhất
<=> 15-x nhỏ nhất
=> 15-x=1
=> x= 14
Giải sơ lược do đã muộn nên bạn thông cảm nhé!! Nếu ko hiểu thì hỏi lại mih nha.