Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua đường thẳng \(\Delta\) với : d: 2x-y+1=0 và \(\Delta\): 3x-4y+2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
31 tháng 5 2021
a) Gọi pt đường thẳng (d) là : \(y=ax+b\left(a\ne0\right)\)
Vì (d) có hệ số góc là 2 \(\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(-1;3\right)\)
\(\Rightarrow3=-2+b\Rightarrow b=5\Rightarrow y=2x+5\)
b) Gọi pt đường thẳng d là \(y=ax+b\left(a\ne0\right)\)
Vì \((d)\parallel (d')\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(3;5\right)\)
\(\Rightarrow5=6+b\Rightarrow b=-1\Rightarrow y=2x-1\)
MN
3 tháng 6 2021
c)
(d) vuông góc với (d') : y = 2x
=> (d) có dạng : y = -2x + b
(d) đi qua M (3,5) :
5 = (-2) . 3 + b
=> b = 10
(d) : y = -2x + 10
CM
8 tháng 5 2019
Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
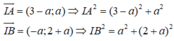
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
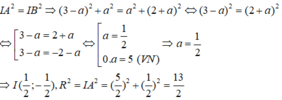
Vậy phương trình đường tròn có dạng:
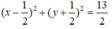
Ta có:
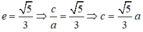
Giả sử elip (E) có dạng:
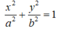
Vì (E) đi qua B nên:
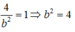
Mà
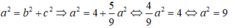
Vậy phương trình chính tắc của elip (E) là:
MH
23 tháng 2 2021
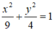
a) Gọi phương trình đường thẳng cần lập là \(y=ax+b\left(d_1\right)\).
Để \(\left(d_1\right)\)//\(\left(d\right)\) thì \(a=2\) \(\Rightarrow\left(d_1\right):y=2x+b\).
Xét phương trình hoành độ giao điểm của \(\left(d_1\right)\) và \(\left(d'\right)\):
\(2x+b=3x-2\Leftrightarrow x=b+2\).
Hai đường thẳng này cắt nhau tại điểm có hoành độ là 2
\(\Leftrightarrow b+2=2\Leftrightarrow b=0\).
Vậy phương trình đường thẳng cần lập là \(\left(d_1\right):y=2x\).
b) Gọi phương trình đường thẳng cần lập là \(y=ax+b\left(d_2\right)\).
\(\left(d_2\right)\perp\left(d'\right)\Leftrightarrow3a=-1\Leftrightarrow a=-\dfrac{1}{3}\)
\(\Rightarrow\left(d_2\right):y=-\dfrac{1}{3}x+b\).
Xét phương trình hoành độ giao điểm của \(\left(d_2\right)\) và \(\left(d\right)\):
\(2x-3=-\dfrac{1}{3}x+b\Leftrightarrow\dfrac{7}{3}x=b+3\Leftrightarrow x=\dfrac{3b+9}{7}\)
\(\Rightarrow y=2x-3=\dfrac{6b-3}{7}\).
Hai đường thẳng này cắt nhau tại điểm có tung độ bằng -1
\(\Leftrightarrow\dfrac{6b-3}{7}=-1\Leftrightarrow6b-3=-7\Leftrightarrow b=-\dfrac{2}{3}\).
Vậy phương trình đường thẳng cần lập là \(\left(d_2\right):y=-\dfrac{1}{3}x-\dfrac{2}{3}\).