Trong không gian với hệ tọa độ Oxyz. Gọi M là tọa độ giao điểm của đường thẳng \(\Delta:\frac{x-2}{-3}=\frac{y}{1}=\frac{z+1}{2}\) và mặt phẳng (P) : x+2y-3z+2=0. Khi đó tọa độ điểm M bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
6 tháng 3 2017
Chọn A
Tìm giao điểm I từ hệ phương trình đường thẳng d và mặt phẳng (P). Viết phương trình đường thẳng IM. Gọi tọa độ điểm M theo tham số của đường thẳng IM rồi xác định tham số đó từ phương trình I M = 4 14

CM
20 tháng 9 2019
Đáp án B
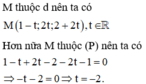
Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

CM
14 tháng 4 2019
Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

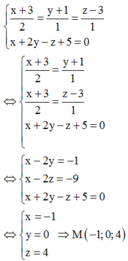
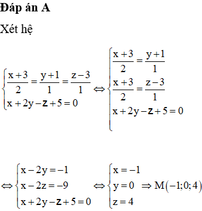

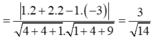

Lời giải:
Gọi tọa độ của \(M=(a,b,c)\)
Vì \(M\in (\Delta)\Rightarrow \frac{a-2}{-3}=\frac{b}{1}=\frac{c+1}{2}=t\)
\(\Rightarrow\left\{\begin{matrix}a=-3t+2\\b=t\\c=2t-1\end{matrix}\right.\)
Mặt khác \(M\in (P)\Rightarrow a+2b-3c+2=0\)
\(\Leftrightarrow -3t+2+2t-3(2t-1)+2=0\)
\(\Leftrightarrow -7t+7=0\Rightarrow t=1\)
Do đó \(M(-1,1,1)\)