Cho tam giác đều ABC. Trên tia đối tia BA lấy điểm M, trên tia đối của tia CB lấy điểm N, trên tia đối của tia AC lấy điểm I sao cho BM = CN = AI.
a, C/m tam giác BMN = tam giác CNI
b, C/m tam giác MNI là tam giác đều
c, C/m điểm cách đều 3 đỉnh tam giác ABC và tam giác MNI là trùng nhau.
(Vẽ hình và C/m)

 Bn tham khảo nhé!
Bn tham khảo nhé!
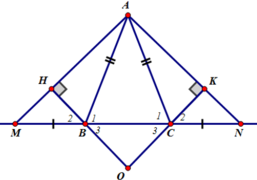

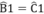
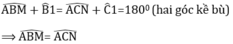
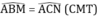
a) Vì \(\Delta\)ABC đều nên \(\widehat{ABC}=\widehat{ACB}=\widehat{BAC}\) và AB = AC = BC.
Ta có: \(\widehat{ABC}\) + \(\widehat{NBM}\) = 180o (kề bù)
\(\widehat{ACB}\) + \(\widehat{ICN}\) = 180o (kề bù)
=> \(\widehat{NBM}\) = \(\widehat{ICN}\)
Lại có: BC + CN = BN
AC + IA = CI
mà BC = AC; CN = IA
=> BN = CI
Xét \(\Delta\)BMN và \(\Delta\)CNI có:
BN = CI (c/m trên)
\(\widehat{NBM}\) = \(\widehat{ICN}\) (c/m trên)
BM = CN (gt)
=> \(\Delta\)BMN = \(\Delta\)CNI (c.g.c)
b) Vì \(\Delta\)BMN = \(\Delta\)CNI (câu a)
=> MN = NI (2 cạnh t/ư)
Lại có:
\(\widehat{ACB}\) + \(\widehat{ICN}\) = 180o (kề bù) \(\widehat{BAC}\) + \(\widehat{MAI}\) = 180o (kề bù) mà \(\widehat{ACB}=\widehat{BAC}\) => \(\widehat{ICN}=\widehat{MAI}\) Ta lại có: AB + BM = AM AC + IA = IC mà AB = AC; BM = IA => AM = IC Xét \(\Delta\)AMI và \(\Delta\)CIN có: AM = CI (c/m trên) \(\widehat{MAI}\) = \(\widehat{ICN}\) (c/m trên) AI = CN (gt) => \(\Delta\)AMI = \(\Delta\)CIN (c.g.c) => MI = IN (2 cạnh t/ư) mà MN = IN (c/m trên) => MI = IN = MN Do đó \(\Delta\)MNI đều.