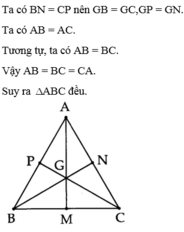
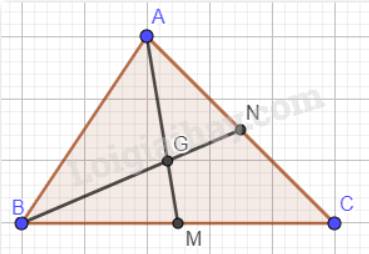
hai đường trung tuyến AM và BN của tam giac abc cắt nhau ở G. Tinh Sabc biết Sabg=336 cm2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 8 2021
Xét ΔANG và ΔCND có
\(\widehat{GAN}=\widehat{DCN}\)
NA=NC
\(\widehat{ANG}=\widehat{CND}\)
Do đó: ΔANG=ΔCND
Suy ra: NG=ND
Xét ΔBAC có
BN là đường trung tuyến ứng với cạnh huyền AC
AM là đường trung tuyến ứng với cạnh huyền BC
BN cắt AM tại G
Do đó: G là trọng tâm của ΔBAC
Suy ra: \(BG=\dfrac{2}{3}BN\)
\(\Leftrightarrow NG=ND=\dfrac{1}{3}BN\)
\(\Leftrightarrow BG=GD\)
hay B và D đối xứng nhau qua G
NT
1
AH
Akai Haruma
Giáo viên
19 tháng 2 2019
Lời giải:
Vì $G$ là giao điểm của hai đường trung tuyến nên $G$ là trọng tâm. Theo tính chất trọng tâm và đường trung tuyến thì \(AG=\frac{2}{3}AM\)
Khi đó:
\(\frac{S_{ABG}}{S_{ABM}}=\frac{AG}{AM}=\frac{2}{3}(1)\)
Mà: \(\frac{S_{ABM}}{S_{ABC}}=\frac{BM}{BC}=\frac{1}{2}(2)\)
Từ \((1);(2)\Rightarrow \frac{S_{ABG}}{S_{ABC}}=\frac{2}{3}.\frac{1}{2}=\frac{1}{3}\)
\(\Rightarrow S_{ABC}=3S_{ABG}=3.336=1008(cm^2)\)