Từ điểm M nằm ngoài đtr(O) vẽ tiếp tuyến MT và cát tuyến MAB. Vẽ đtr(O') ngoại tiếp tam giác MAB, từ M vẽ tiếp tuyến xy của (O'). Cm rằng:
a/ MT2 = MA.MB
b/ BT // xy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét đường tròn (O;R) có \(\widehat{MTA}\)là góc tạo bởi tiếp tuyến MT (tiếp điểm là T) và dây cung TA \(\Rightarrow\widehat{MTA}=\frac{1}{2}sđ\widebat{TA}\)
Mà \(\widehat{MBT}\)là góc nội tiếp chắn cung TA \(\Rightarrow\widehat{MBT}=\frac{1}{2}sđ\widebat{TA}\)
\(\Rightarrow\widehat{MTA}=\widehat{MBT}\left(=\frac{1}{2}sđ\widebat{TA}\right)\)
Xét \(\Delta MTA\)và \(\Delta MBT\), ta có: \(\widehat{BMT}\)chung; \(\widehat{MTA}=\widehat{MBT}\left(cmt\right)\)
\(\Rightarrow\Delta MTA~\Delta MBT\left(g.g\right)\)\(\Rightarrow\frac{MT}{MB}=\frac{MA}{MT}\Rightarrow MT^2=MA.MB\)(1)
Hoàn toàn tương tự, ta có \(MT^2=MC.MD\)(2)
Vì MT là tiếp tuyến tại T của (O) \(\Rightarrow MT\perp OT\)tại T \(\Rightarrow\Delta OMT\)vuông tại T
\(\Rightarrow OM^2=MT^2+OT^2\)\(\Rightarrow MT^2=OM^2-OT^2\)
Đồng thời MT là tiếp tuyến tại T của (O;R) \(\Rightarrow OT=R\)
Như vậy ta có \(MT^2=OM^2-R^2\)(3)
Từ (1), (2) và (3) ta có đpcm.

Xét ΔOTM vuông tại T có \(OM^2=OT^2+TM^2\)
=>\(TM^2=OM^2-OT^2\)
=>\(MT^2=d^2-R^2\left(1\right)\)
Xét (O) có
\(\widehat{MTA}\) là góc tạo bởi tiếp tuyến TM và dây cung TA
\(\widehat{TBA}\) là góc nội tiếp chắn cung TA
Do đó: \(\widehat{MTA}=\widehat{TBA}\)
=>\(\widehat{MTA}=\widehat{MBT}\)
Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MT^2=d^2-R^2\)
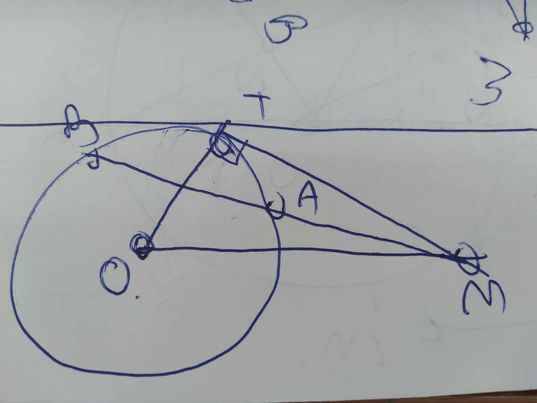

Xét ΔOTM vuông tại T có \(OM^2=OT^2+TM^2\)
=>\(TM^2=OM^2-OT^2\)
=>\(MT^2=d^2-R^2\left(1\right)\)
Xét (O) có
\(\widehat{MTA}\) là góc tạo bởi tiếp tuyến TM và dây cung TA
\(\widehat{TBA}\) là góc nội tiếp chắn cung TA
Do đó: \(\widehat{MTA}=\widehat{TBA}\)
=>\(\widehat{MTA}=\widehat{MBT}\)
Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MT^2=d^2-R^2\)
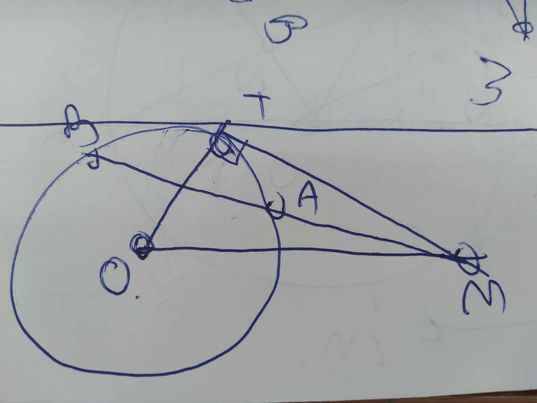

Xin lỗi bạn!
Mk mới học lớp 8 thôi ak!
Chúc bạn có câu trả lời sớm nha!
Kb nhá ^_^
làm gì có tam giác MAB bạn
- Đề bài sai rồi bạn.