Có bao nhiêu số nguyên n thỏa mãn điều kiện sau
(n2-3).(n2-36) < 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow3< =n^2< =36\)
mà n là số nguyên
nên \(n^2\in\left\{4;9;16;25;36\right\}\)
hay \(n\in\left\{2;-2;3;-3;4;-4;5;-5;6;-6\right\}\)
Vậy: Có 10 số nguyên n thỏa mãn bài toán

a)\(n^2-3n^2-36=0\Leftrightarrow-2n^2-36=0\Leftrightarrow-2n^2=36\Leftrightarrow n^2=-18\)
mà \(n^2\ge0\forall n\)=> không có số nguyên nào thỏa mãn\(n^2-3n^2-36=0\)
a)\(n^2-3n^2-36< 0\Leftrightarrow-2n^2-36< 0\Leftrightarrow-2n^2< 36\Leftrightarrow n^2>-18\)
=>Vậy \(n^2-3n^2-36< 0\) với mọi số tự nhiên n


aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

Đáp án A
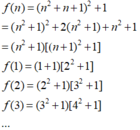
= > U n = ( 1 2 + 1 ) ( 2 2 + 1 ) . ( 3 2 + 1 ) ( 4 2 + 1 ) ... [ ( 2 n − 1 ) 2 + 1 ] [ ( 2 n ) 2 + 1 ] ( 2 2 + 1 ) ( 3 2 + 1 ) . ( 4 2 + 1 ) ( 5 2 + 1 ) ... [( 2 n ) 2 + 1 ] [ ( 2 n + 1 ) 2 + 1 ] = > U n = 2 ( 2 n + 1 ) 2 + 1


\(\left(n^2-3\right)\left(n^2-36\right)=0\)
\(\Rightarrow\orbr{\begin{cases}n^2-3=0\\n^2-36=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}n^2=3\\n^2=36\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}n\in\left\{\pm\sqrt{3}\right\}\\n\in\left\{\pm6\right\}\end{cases}}\)
Vậy....
để (n^2-3)(n^2-36)=0
=>n^2-3=0 và n^2-36=0
=>n^2=3 và n^2=36
=>n= + - căn 3 và n= -6; 6
\(\left(n^2-3\right)\left(n^2-36\right)< 0\)
\(\Leftrightarrow3< n^2< 36\)
mà n là số nguyên
nên \(n^2\in\left\{4;9;16;25\right\}\)
hay \(n\in\left\{2;-2;3;-3;4;-4;5;-5\right\}\)