Biết x tỉ lệ thuận với y theo hệ số tỉ lệ là 3. Hỏi x+y có tỉ lệ với y không và theo hệ số tỉ lệ là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
. Hỏi x tỉ lệ thuận với y theo hệ số tỉ lệ là bao nhiêu?
. Hỏi y tỉ lệ thuận với x theo hệ số tỉ lệ là bao nhiêu?
ND
Nguyễn Đức Trí
VIP
13 tháng 9 2023
\(\left\{{}\begin{matrix}y=-0,4x\\x=10z\end{matrix}\right.\)
\(\Rightarrow y=-0,4.10z=-4z\)
Nên y tỉ lệ thuận với z và có tỉ lệ là -4.
CM
25 tháng 6 2017
Vì x tỉ lệ thuận với y theo hệ số tỉ lệ là 2,7 nên x = 2,7y
Vì x tỉ lệ thuận với z theo hệ số tỉ lệ là 3 nên x = 3z
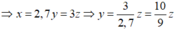
Chọn đáp án A
CM
23 tháng 5 2019
Vì x tỉ lệ thuận với y theo hệ số tỉ lệ là 0,6 nên x = 0,6y
Vì y tỉ lệ thuận với z theo hệ số tỉ lệ là 3 nên y = 3z
⇒ x = 0,6y = 0,6.(3z) = 1,8z
Vậy x tỉ lệ thuận với z theo hệ số tỉ lệ là 1,8
Chọn đáp án C
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Vì y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = a.x
Vì x tỉ lệ thuận với z theo hệ số tỉ lệ b nên x = b.z
Do đó, y = a.x = a.(b.z ) = (a.b).z ( a.b là hằng số vì a,b là các hằng số)
Vậy y có tỉ lệ thuận với z và hệ số tỉ lệ là a.b
27 tháng 10 2016
Vì y tỉ lệ thuận với x theo hệ số tỉ lệ là 3 nên y = 3 . x (1)
Vì x tỉ lệ thuận với z theo hệ số tỉ lệ là \(\frac{-3}{5}\) nên x = \(\frac{-3}{5}\) . z (2)
=> \(\frac{z}{y}\) = \(\frac{z}{3.x}\) = \(\frac{z}{3.\left(\frac{-3}{5}\right).z}\) = \(\frac{z}{\frac{-9}{5}.z}\) = \(\frac{1}{\frac{-9}{5}}\) = 1 . (\(\frac{-5}{9}\)) = \(\frac{-5}{9}\)
Vậy z có tỉ lệ thuận với y và hệ số tỉ lệ là \(\frac{-5}{9}\)
Lời giải:
Theo bài ra ta có:
$x=3y$
$x+y=3y+y=4y$
$\Rightarrow x+y$ tỉ lệ với $y$ theo hệ số tỉ lệ bằng $4$.