tìm giá trị nhỏ nhất của hàm số y=4/x+9/(1-x) với x trong khoảng từ 0 đến 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\left|1-x\right|+\left|x+2\right|-3\ge\left|1-x+x+2\right|-3=0\)
Dấu ''='' xảy ra khi \(\left(1-x\right)\left(x+2\right)\ge0\Leftrightarrow-2\le x\le1\)
mà x là số nguyên nên x = -2 ; -1 ; 0 ; 1

\(A=\left|x+1\right|+\left|y-2\right|+5\ge5\)
Dấu ''='' xảy ra khi x = -1 ; y = 2
Vậy ...


Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
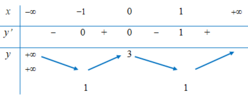
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.

\(f\left(x\right)=\dfrac{4}{x}+\dfrac{x-1+1}{1-x}=\dfrac{4}{x}+\dfrac{1}{1-x}-1\)
\(f\left(x\right)\ge\dfrac{\left(2+1\right)^2}{x+1-x}-1=8\)
\(f\left(x\right)_{min}=8\) khi \(x=\dfrac{2}{3}\)

Đáp án C
Lưu ý: Đề không cho tìm max – min trên đoạn nên ta không thể so sánh các giá trị như vậy
Cách giải: Lập BBT và ở đây kết luận được giá trị nhỏ nhất của hàm số là 1 , nhưng hàm số không có giá trị lớn nhất.

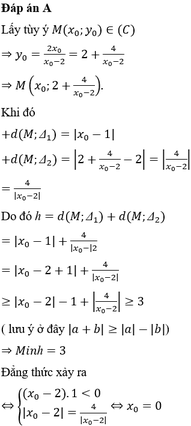
\(\left\{\begin{matrix}A=\frac{4}{x}+\frac{9}{1-x}\left(1\right)\\0< x< 1\left(2\right)\end{matrix}\right.\) Lần trước gặp bài này lớp 8 mình đã giải theo cách lớp 8.
Dùng Bất đẳng thức
Từ (2) \(\Rightarrow\left\{\begin{matrix}\frac{4}{x}>0\\\frac{9}{\left(1-x\right)}>0\end{matrix}\right.\) \(\left(1\right)\Leftrightarrow A=\frac{2^2}{x}+\frac{3^2}{1-x}\ge\frac{\left(2+3\right)^2}{\left(x\right)+\left(1-x\right)}=\frac{25}{\left(1\right)}=25\)
Đẳng thức khi: \(9x=4\left(1-x\right)\Rightarrow10x=4\Rightarrow x=\frac{2}{5}\\ \) Thỏa mãn đk (2)
Vậy: \(A_{min}=25...khi...x=\frac{2}{5}\)