Tìm 3 số nguyên dương x , y , z . Sao cho 1/x + 1/y + 1/z = 2 .
Toán lớp 7 . Đề ôn thi học kì 1 của lớp mk đó ạ . Khó quá giải hộ mình vs . Đaq cần gấp ạ !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MX
0
17 tháng 1 2020
Link nè: https://dethi.violet.vn/present/show/entry_id/11006794\
Chúc bạn hoc tốt ~ !
CM
6 tháng 12 2017
Đáp án B
Phương pháp : Chia hai trường hợp :
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi.
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi.
Cách giải : Ω = C 2 n 3
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi. Có C n 2 . C n 1 cách
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi. Có C n 3 cách
Gọi A là biến cố học sinh TWO không phải thi lại
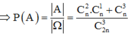
Đến đây chọn một giá trị bất kì của n rồi thay vào là nhanh nhất, chọn n =10 , ta tính được P ( A ) = 1 2
24 tháng 8 2017
ta có: a+b+c=1
<=>(a+b+c)^2=1
<=>ab+bc+ca=0 (1)
mặt khác: áp dụng tính chất dãy tỉ số bằng nhau ta có:
x/a=y/b=z/c=(x+y+z)/(a+b+c)=x+y+z
<=> x=a(x+y+z) ; y=b(x+y+z) ; z=c(x+y+z)
=>xy+yz+zx=ab(x+y+z)^2+bc(x+y+z)^2+ca(x...
<=>xy+yz+zx=(ab+bc+ca)(x+y+z)^2 (2)
từ (1) và (2) ta có đpcm
30 tháng 11 2023
\(A=log_m\left(8m\right)=log_mm+log_m8\)
\(=1+log_m8\)
\(=1+\dfrac{1}{log_8m}=1+\dfrac{1}{log_{2^3}m}=1+\dfrac{1}{\dfrac{1}{3}\cdot log_2m}\)
\(=1+\dfrac{1}{\dfrac{1}{3}a}=1+1:\dfrac{a}{3}=1+\dfrac{3}{a}=\dfrac{a+3}{a}\)
=>Chọn A
lớp 7 sao giải đc