Một con lắc lò xo dđđh với quỹ đạo 10cm, lò xo có độ cứng k dao động theo phương ngang. khi con lắc ở vị trí lò xo có chiều dài lớn nhất, giữ điểm chính giữa lò xo. Biên độ dđ của hệ :
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
22 tháng 2 2019
Chọn A
+ Biên độ dao động ban đầu của con lắc A = 0,5L = 8 cm.
→ Áp dụng kết quả của bài toán trên, với m = 2 và n = 1, ta có A ' = m n + 1 2 m n + 1 A = 2.1 + 1 2.2 1 + 1 8 = 2 6 cm.
VT
9 tháng 5 2018
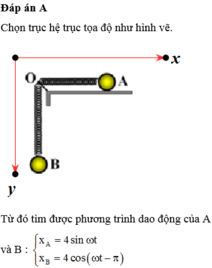
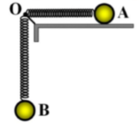
Có : A B 2 = O A 2 + O B 2 = 34 + x A 2 + 34 + x B 2 = x A 2 + x B 2 + 68 x A + x B + 2 . 34 2 = 16 sin 2 ω t + 16 cos 2 ω t + 68 4 sin ω t - 4 cos ω t + 2 . 34 2 = 16 + 68 . 4 2 cos ω t + φ + 2 . 34 2 ⇒ A B m a x = 16 + 68 . 4 2 + 2 . 34 2 ≈ 52 c m
VT
20 tháng 9 2017
Chọn A
Tại thời điểm cố định lò xo ta có E d = n E t E d + E t = E → E t = E n + 1 E d = n E n + 1
+ Vì thế năng đàn hồi của lò xo phân bố đều trên mỗi đơn vị chiều dài, do vậy thế năng của hệ dao động mới là E ' t = E t m = E m n + 1
+ Cơ năng của hệ dao động mới: E ' = E ' t + E ' d = E m n + 1 + n E n + 1 = 1 2 k ' A ' 2
Trong đó k′ = mk là độ cứng của phần lò xo tham gia vào dao động của vật lúc sau.
→ Biến đổi toán học ta thu được tỉ số A ' A = m n + 1 2 m n + 1
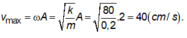
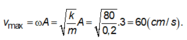
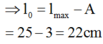
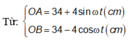
Biên độ ban đầu: A1=10/2=5 (cm)
Khi con lắc ở vị trí lò xo có chiều dài lớn nhất, giữ điểm chính giữa lõ xo thì độ cứng phần lò xo gắn với vật là k/2
Vì cơ năng được bảo toàn nên ta có
\(\frac{1}{2}k_1A_1^2=\frac{1}{2}k_2A_2^2\Leftrightarrow k.0,05^2=2k.A_2^2\Leftrightarrow A_2=\frac{0,05}{\sqrt{2}}\left(m\right)\)