Cho
a1+a2+a3+a4+...+a19+a20+a21=10
biết rằng
a1+a2=a3+a4=...=a12+a20=a20+a21=8
Tìm a20
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QH
1
10 tháng 1 2018
\(a_1+a_2+a_3+a_4+...+a_{19}+a_{20}+a_{21}=10\)
\(\Rightarrow\left(a_1+a_2\right)+\left(a_3+a_4\right)+...+\left(a_{19}+a_{20}\right)+a_{21}=10\)
\(\Rightarrow1+1+...+1+a_{21}=10\)
\(\Rightarrow10+a_{21}=10\)
\(\Rightarrow a_{21}=0\)
Mà \(a_{20}+a_{21}=2\Leftrightarrow a_{20}=2\)
LT
1
27 tháng 12 2017
Ta có: a1+a2=2; a3+a4=2;.................; a19+a20=2; a20+a21=2
=> a1+a2+a3+a4+...........+ a19+a20+ a20+a21=2+2+2+2+....+2(11 số hạng 2)=2.11=22
=> a1+a2+a3+a4+.........+a19+a20+a21=22- a20
Mà a1+a2+a4+.............+a21=10 => a20=22-10=12
Vậy a20=12
Nhớ k hộ mình nha
Mong quản lí OLM k cho em
Cảm ơn tấm lòng của mọi người
NT
0
I
25 tháng 2 2020
Ta có a1 +a2+...+a20 <0
Lại có a2+a3+a4 >0;
a5 +a6+a7 >0;
a8+a9+a10>0;
a11+a12+a13>0;
a15+a16+a17>0;
a18 +a19+a20>0;
a1>0
=> a14<0;
Lại có a1+a2+a3 >0;
a4+a5+a6>0;
....
a10+a11+a12>0;
a15+a16+a17>0;
a18+a19+a20>0;
=> a13+a14<0;
mà a12+a13+a14>0;
=>a12>0;
=> a1.a12>0;
a1.a14+a14.a12<0;
=>a1.a14+a14.a12<a1.a12
24 tháng 4 2016
sai đề : phải là: a1.a14+a14.a12<a1.a12 nếu thế thì giải như sau
Ta có : a1 + (a2 + a3 + a4) + … + (a11 + a12 + a13) + a14 + (a15 + a16 + a17) + (a18 + a19 + a20) < 0 ; a1 > 0 ; a2 + a3 + a4 > 0 ; … ; a11 + a12 + a13 > 0 ; a15 + a16 + a17 > 0 ; a18 + a19 + a20 > 0 => a20 < 0.
Cũng như vậy : (a1 + a2 + a3) + … + (a10 + a11 + a12) + (a13 + a14) + (a15 + a16 + a17) + (a18 + a19 + a20) < 0 => a13 + a14 < 0.
Mặt khác, a12 + a13 + a14 > 0 => a12 > 0.
Từ các điều kiện a1 > 0 ; a12 > 0 ; a14 < 0 => a1.a14 + a14a12 < a1.a12 [dpcm]
CM
5 tháng 1 2018
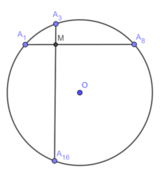
Gọi giao điểm của A 1 A 8 và A 3 A 16 là M
Vì đường tròn được chia thành 20 cung
bằng nhau nên số đo của mỗi cung là :
360 ° : 20 = 18 °
2 tháng 12 2018
Câu hỏi của Vu Kim Ngan - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé!
23 tháng 11 2021
\(\dfrac{a_1}{a_2}=\dfrac{a_2}{a_3}=...=\dfrac{a_{2013}}{a_{2014}}=\dfrac{a_{2014}}{a_1}=\dfrac{a_1+a_2+...+a_{2014}}{a_1+a_2+...+a_{2014}}=1\\ \Leftrightarrow a_1=a_2=...=a_{2014}\\ \Leftrightarrow Q=\dfrac{\left(2014a_1\right)^2}{a_1^2\left(1+2+...+2014\right)}=\dfrac{2014^2\cdot a_1^2}{a_1^2\cdot\dfrac{2015\cdot2014}{2}}=\dfrac{2\cdot2014^2}{2015\cdot2014}=\dfrac{2\cdot2014}{2015}=...\)