tìm tâm và bán kính mặt cầu ngoại tiếp hình lăng trụ tam giác có tất cả các cạnh bằng a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 8 2018
Bán kính đường tròn ngoại tiếp đáy của hình lăng trụ là 
Khi đó bán kính mặt cầu ngoại tiếp hình lăng trụ đó là
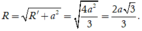
Chọn B.
CM
15 tháng 5 2019
Đáp án C
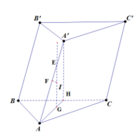
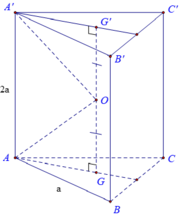
Cho lăng trụ tam giác đều ABC.A'B'C'.
Gọi G, G; lần lượt là tâm của hai đáy ABC và A'B'C'.
Ta có GG' chính là trục của các tam giác ABC và A'B'C' .
Gọi O là trung điểm của GG' thì O cách đều 6 đỉnh của hình lăng trụ
nên là tâm của mặt cầu ngoại tiếp hình lăng trụ. Bán kính mặt cầu là R = OA.
Xét tam giác OAG vuông tại G, ta có:
CM
21 tháng 4 2018
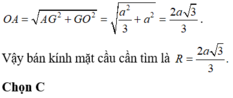
Đáp án A
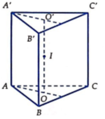
Gọi OO' lần lượt là tâm các tam giác ABC và A'B'C'
Gọi I là trung điểm OO'=> Bán kính mặt cầu ngoại tiếp lăng trụ là R = IA
A O = 2 3 . a 3 2 = a 3 I O = 1 2 A A ' = a 2 ⇒ R 2 = A O 2 + I O 2 = 7 a 2 12
Diện tích mặt cầu ngoài tiếp lăng trụ S = 4 π R 2 = 7 π a 2 3
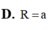
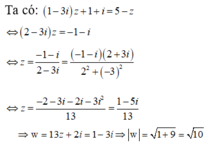
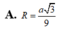
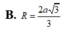
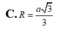
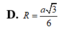
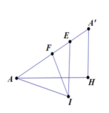
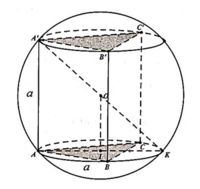
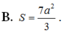
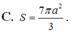
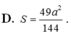
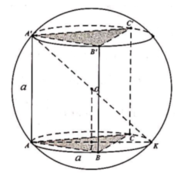
gọi I là tâm đường tròn ngoại tiếp đáy.Do đáy là tam giác đều nên I là trọng tâm
suy ra IA =\( \frac{a\sqrt{3}}{2}\) (giả sử hình lăng trụ là ABC\(A^, B^,C^,\) có cạnh là a)
trong mp(SAI),từ I kẻ đường thẳng d vuông góc vs đáy .Gọi N là trung điểm SA,từ N kẻ đt vuông góc vs SA,cắt d tại O.
O là tâm mặt cầu cần tìm.R=OA=\(\sqrt{OI^2 +AI^2}\)=a
mình xin lỗi chắc tại hôm qua làm muộn đén khuya buồn ngủ quá nên mình làm nhầm.bạn thayS là \(A^,\) cho mình nhé.vậy nên kết quả tìm bán kính sai rồi. nhưng cách làm vẫn tương tự nhé
R=\(\sqrt{0,5^2 a^2 +\frac{a^2}{3}}\) =\(\frac{\sqrt{21}a}{6}\) thông cảm nhé