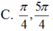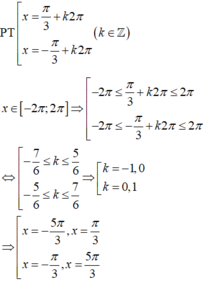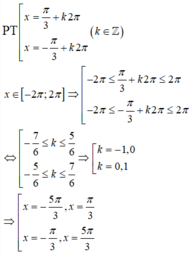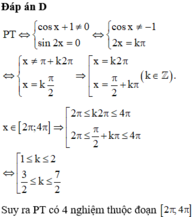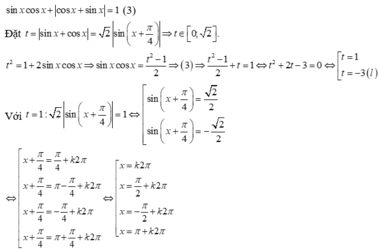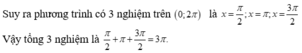số nghiệm của phương trình \(\frac{sin3x}{cosx+1}\)=0 thuộc đoạn [2π;4π] là bao nhiêu ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 8 2017
Đáp án A
Cách 1:
Bằng phương pháp thử ta được nghiệm của phương trình sin 3 x − cos x = 0 thuộc đoạn − π 2 ; 3 π 2 là 5 π 4
Cách 2:
Ta có: sin 3 x = cos x ⇔ sin 3 x = sin π 2 − x
⇔ 3 x = π 2 − x + k 2 π 3 x = π 2 + x + k 2 π ⇔ x = π 8 + k π 2 x = π 4 + k π k ∈ ℤ
Vậy nghiệm lớn nhất thuộc đoạn − π 2 ; 3 π 2 là 5 π 4
CM
2 tháng 1 2019
Vì các nghiệm của phương trình thuộc khoảng
(
0
;
2
π
)
nên nghiệm của phương trình là 
PT
1
CM
8 tháng 9 2018
Đáp án D
P T ⇔ cos x + 1 ≠ 0 sin 2 x = 0 ⇔ cos x ≠ − 1 2 x = k π ⇔ x ≠ π + k 2 π x = k π 2 ⇒ x = k 2 π x = π 2 + k π k ∈ ℤ .
x ∈ 2 π ; 4 π ⇒ 2 π ≤ k 2 π ≤ 4 π 2 π ≤ π 2 + k π ≤ 4 π ⇔ 1 ≤ k ≤ 2 3 2 ≤ k ≤ 7 2
Suy ra PT có 4 nghiệm thuộc đoạn 2 π ; 4 π .
