cho 4,7g hỗn hợp al và ca tác dụng vừa đủ với 5,7g flo và 35,5g clo. tính kl ca và al
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
4 tháng 1 2021
Gọi \(n_{Mg} = a(mol) ; n_{Al} = b(mol)\\ \Rightarrow 24a + 27b = 5,7(1)\)
\(Mg^0 \to Mg^{+2} + 2e\\ Al^0 \to Al^{+3} + 3e\\ O_2 + 4e \to 2O^{-2}\\ Cl_2 + 2e \to 2Cl^-\)
Bảo toàn electron : \(2n_{Mg} + 3n_{Al} = 2a + 3b = 4n_{O_2} + 2n_{Cl_2} = 1,2(mol)\)(2)
Từ (1)(2) suy ra : a = -0,85< 0 ⇒ Sai đề
4 tháng 1 2021
X{Mg, Al} + {Cl2, O2} → Z
Áp dụng định luật BTKL: mCl2 + mO2 = mZ – mX = 19,7 – 7,8 = 11,9 gam
Theo đề bài ta có hệ phương trình:
⎧⎪⎨⎪⎩nCl2+nO2=5,622,4=0,2571nCl2+32nO2=11,9→{nCl2=0,1nO2=0,15{nCl2+nO2=5,622,4=0,2571nCl2+32nO2=11,9→{nCl2=0,1nO2=0,15
Đặt số mol của Mg và Al lần lượt là x và y (mol)
- Khối lượng hỗn hợp: 24x + 27y = 7,8 (1)
- Bảo toàn e: 2nMg + 3nAl = 2nCl2 + 4nO2 => 2x + 3y = 0,1.2 + 0,15.4 hay 2x + 3y = 0,8 (2)
Giải (1) và (2) thu được x = 0,1 và y = 0,2
=> %mAl = 0,2.27/7,8 = 69,23%
23 tháng 2 2022
Sửa: $V_{H_2}=7,168(l)$
$a\bigg)$
Đặt $n_{Mg}=x;n_{Fe}=y;n_{Al}=z$
$\to 24x+56y+27z=9,52(1)$
$n_{H_2}=\dfrac{7,168}{22,4}=0,32(mol)$
$n_{Cl_2}=\dfrac{8,064}{22,4}=0,36(mol)$
BTe: $x+y+1,5z=n_{H_2}=0,32(2)$
BTe: $x+1,5y+1,5z=n_{Cl_2}=0,36(3)$
Từ $(1)(2)(3)\to x=0,12(mol);y=0,08(mol);z=0,08(mol)$
$\to \begin{cases} \%m_{Mg}=\dfrac{0,12.24}{9,52}.100\%=30,25\%\\ \%m_{Fe}=\dfrac{0,08.56}{9,52}.100\%=47,06\%\\ \%m_{Al}=100-47,06-30,25=22,69\% \end{cases}$
$b\bigg)$
Bảo toàn H: $n_{HCl}=2n_{H_2}=0,64(mol)$
$\to C_{M_{HCl}}=\dfrac{0,64}{0,2}=3,2M$
$\to a=3,2$
$c\bigg)$
Dung dịch sau gồm $MgCl_2,FeCl_2,AlCl_3$
Bảo toàn $Mg,Al,Fe:n_{MgCl_2}=0,12(mol);n_{AlCl_3}=n_{FeCl_2}=0,08(mol)$
$\to C_{M_{MgCl_2}}=\dfrac{0,12}{0,2}=0,6M$
$\to C_{M_{AlCl_3}}=C_{M_{FeCl_2}}=\dfrac{0,08}{0,2}=0,4M$
23 tháng 2 2022
$a\bigg)$
Đặt $n_{Mg}=x;n_{Fe}=y;n_{Al}=z$
$\to 24x+56y+27z=9,52(1)$
$n_{H_2}=\dfrac{14,336}{22,4}=0,64(mol)$
$n_{Cl_2}=\dfrac{8,064}{22,4}=0,36(mol)$
BTe: $x+y+1,5z=n_{H_2}=0,64(2)$
BTe: $x+1,5y+1,5z=n_{Cl_2}=0,36(3)$
Từ $(1)(2)(3)\to$ nghiệm âm, xem lại đề
3 tháng 4 2022
Gọi nAl = nZn = a (mol)
\(n_{H_2}=\dfrac{13,44}{22,4}=0,6\left(mol\right)\)
PTHH: 2Al + 6HCl --> 2AlCl3 + 3H2
a---------------------->1,5a
Zn + 2HCl --> ZnCl2 + H2
a--------------------->a
=> 1,5a + a = 0,6
=> a = 0,24 (mol)
=> mhh = 0,24.27 + 0,24.65 = 22,08 (g)
3 tháng 4 2022
Gọi \(n_{Al}=n_{Zn}=a\left(mol\right)\)
PTHH:
2Al + 6HCl ---> 2AlCl3 + 3H2
a a
Zn + 2HCl ---> ZnCl2 + H2
a a
\(\rightarrow22,4\left(a+a\right)=13,44\\ \Leftrightarrow a=0,3\left(mol\right)\\ \rightarrow\left\{{}\begin{matrix}m_{Al}=0,3.27=8,1\left(g\right)\\m_{Zn}=0,3.65=19,5\left(g\right)\end{matrix}\right.\\ \rightarrow m_{hh}=8,1+19,5=27,6\left(g\right)\)
SS
18 tháng 1 2016
Cu ko pư => mCu = 3.2
=> mAl, Fe = 14.2 - 3.2 = 11
2Al + 6HCl --------> 2AlCl3 + 3H2
Fe + 2HCl ----------> FeCl2 + H2
nH2 = 8.96/22.4 = 0.4
Ta có hpt
27x + 56y = 11
1.5x + y = 0.4
Giải hpt
x = 0.2
y = 0.1
a.
mAl = 27*0.2 = 5.4
%mAl = 5.4*100/14.2 = 38%
%mCu = 3.2*100/14.2 = 22.5%
=> %mFe = 100 - (38 - 22.5) = 39.5%
b.
nHCl = 6x + 2y = 1.4
=> V HCl = 1.4/1.5 = 0.93M
Ý cuối ko hỉu cho b(g) sao tìm a
1 tháng 3 2019
Đáp án A
Ta có mX + mY = mZ => 7,8 + mY = 19,7
mY = 11,9 (g)
Gọi 
Ta có x + y = 
= 0,25(mol) (1)
= 71x + 32y = 1,9 (2)
Giải (1) và (2) ta có x = 0,1 (mol); y = 0,15(mol)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
5 tháng 1 2022
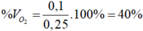
\(\text{Đ}\text{ặt}:n_{Mg}=a\left(mol\right);n_{Al}=1,5a\left(mol\right)\\ \Rightarrow24a+27.1,5a=12,9\\ \Leftrightarrow a=0,2\left(mol\right)\\\Rightarrow n_{Mg}=0,2\left(mol\right);n_{Al}=0,3\left(mol\right)\\ 2Al+3Cl_2\rightarrow\left(t^o\right)2AlCl_3\\ Mg+Cl_2\rightarrow\left(t^o\right)MgCl_2\\ n_{AlCl_3}=n_{Al}=0,3\left(mol\right);n_{MgCl_2}=n_{Mg}=0,2\left(mol\right)\\ m_{mu\text{ố}i}=m_{MgCl_2}+m_{AlCl_3}=95.0,2+0,3.133,5=59,05\left(g\right)\)
Đây là bài 1
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
5 tháng 1 2022
B2:
\(n_{H_2}=0,4\left(mol\right)\\ n_{Cl_2}=0,45\left(mol\right)\\ \text{Đ}\text{ặt}:n_{Al}=x\left(mol\right);n_{Fe}=y\left(mol\right)\left(x,y>0\right)\\ 2Al+6HCl\rightarrow2AlCl_3+3H_2\\ Fe+2HCl\rightarrow FeCl_2+H_2\\ 2Al+3Cl_2\rightarrow\left(t^o\right)2AlCl_3\\ 2Fe+3Cl_2\rightarrow\left(t^o\right)2FeCl_3\\ \Rightarrow\left\{{}\begin{matrix}1,5x+y=0,4\\1,5x+1,5y=0,45\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0,2\\y=0,1\end{matrix}\right.\\ \Rightarrow m=m_{Al}+m_{Fe}=27x+56y=27.0,2+56.0,1=11\left(g\right)\)
25 tháng 2 2021
a) PTHH: \(Ca+H_2SO_4\rightarrow CaSO_4+H_2\uparrow\)
\(Fe+H_2SO_4\rightarrow FeSO_4+H_2\uparrow\)
\(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\uparrow\)
b) Ta có: \(\Sigma n_{H_2}=\dfrac{11,2}{22,4}=0,5\left(mol\right)\)
Theo các PTHH, ta thấy \(n_{H_2SO_4}=n_{H_2}=0,5\left(mol\right)\)
\(\Rightarrow m_{H_2SO_4}=0,5\cdot98=49\left(g\right)\)
Mặt khác: \(m_{H_2}=0,5\cdot2=1\left(g\right)\)
Bảo toàn khối lượng: \(m_{hh}=m_{muối}+m_{H_2}-m_{H_2SO_4}=68+1-49=20\left(g\right)\)
mình nghĩ nên chỉnh lại cái đề, hình như đề sai, 6,7g hỗn hợp kim loại và 3,55 g clo (5,7 g flo mà lại 35,5g clo thì hơi quá)
Cl2 + 2e --> 2Cl-
0,1....0,2
F2 + 2e ---> 2F-
0,15...0,3
Al nhường 3e, Ca nhường 2e, theo định luật bảo toàn e: tổng e nhường bằng tổng e nhận => 3x+2x=0,2+0,3=0,5 (1)
theo đề => 27x+ 40y= 6,7
giải hệ
=>x=0,1;
y=0,1
=>mAl=2,7 g
mCa=4 g
cho mình sửa lại, đề chỉ sai ở chỗ 35,5g, theo mình nghĩ là 3,55g khí Cl mới đúng
F2 + 2e ---> 2F-
0,15.. 0,3
Cl2 + 2e ---> 2Cl-
0,05...0,1
Al nhường 3e, Ca nhường 2e, áp dụng định luật bảo toàn e, tổng e nhường = tổng e nhận
=> 3x + 2y = 0,4 (1)
theo đề : 27x +40y = 4,7 (2)
từ (1) và (2)
=> x= 0,1
y=0,05
=> mAl = 2,7(g);mCa=2(g)