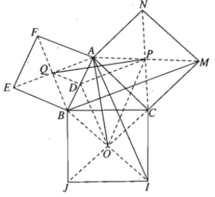
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'
cho tam giác abc có 3 góc nhọn. phía ngoài tam giác abc dựng các hình vuông abed, bcgf, achi có tâm lần lượt là c’, a’, b’. chứng minh: aa' = b'c'