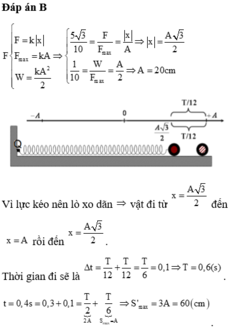
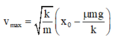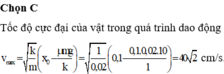"Câu 27. Một con lắc lò xo dao động không ma sát trên mặt phẳng ngang, biết rằng trong quá trình dao động quãng đường đi lớn nhất trong khoảng thời gian denta t < T/2 là 20cm và quãng đường đi nhỏ nhất trong khoảng thời gian denta t là 40 - 20 căn 3 Biên độ dao động của vật là"
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B.
Chu kì:
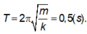
Thời gian:
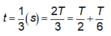
Khi đi theo chiều âm thì lực ma sát hướng theo chiều dương nên có thể xem vị trí cân bằng đến I, còn khi đi theo chiều dương, lực ma sát hướng theo chiều âm thì vị trí cân bằng dịch đến I’ (sao cho: 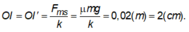
Độ giảm biên độ sau mỗi nửa chu kì:
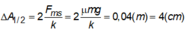
nên
![]()
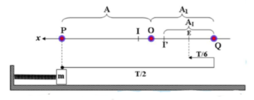
Hiện tượng xảy ra có thể mô ta như sau: Vật đi từ P đến Q mất thời gian T/2 và đi được quãng đường PQ = A + A1 = 16 cm. Vật đi từ Q đến E mất thời gian T/6, lúc này tâm dao động là I’ nên E là trung điểm của QI’, biên độ dao động so với I’ là A1 = 1/3 s là S = PQ + QE = 18 cm.
Bình luận: Bài toàn trên sẽ khó hiểu hơn nếu t Q E ≠ T / 6 Lúc này,
![]()
nên
![]()

Hướng dẫn:
+ Độ biến dạng của lò xo tại vị trí cân bằng tạm x 0 = μ m g k = 0 , 1.0 , 1.10 100 = 10 − 3 m
→ Biên độ dao động của vật trong nửa chu kì đầu tiên A 1 = X 0 – x 0 .
Cứ sau mỗi nửa chu kì, kể từ nửa chu kì thứ 2 biên độ của vật dao động so với các vị trí cân bằng tạm sẽ giảm 2 x 0 .
→ Ta xét tỉ số A 1 2 x 0 = X 0 − x 0 2 x 0 = 0 , 1 − 10 − 3 2.10 − 3 = 49 , 5
→ Biên độ của vật sau 49 nửa chu kì tiếp theo là A 49 = A 1 – ( 49 . 2 + 1 ) x 0 = 1 m m → vật tắt dần tại đúng vị trí lò xo không biến dạng.
+ Áp dụng định luật bảo toàn và chuyển hóa năng lượng ta có 1 2 k X 0 2 = μ m g S → S = k X 0 2 2 μ m g = 100.0 , 1 2 2.0 , 1.0 , 1.10 = 5 m
Đáp án B

Đáp án A
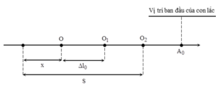
+ Gọi Δ l 0 là độ biến dạng của lò xo ứng với cường độ điện trường có độ lớn E
Cứ mỗi lần điện trường tăng lên một lượng E thì vị trí cân bằng của con lắc dịch chuyển về phía phải một đoạn Δ l 0 và biên độ sẽ giảm đi một lượng cũng đúng bằng Δ l 0 .Trong 4 s khi đó vị trí cân bằng của con lắc bây giờ trùng với vị trí ban đầu do đó con lắc sẽ dừng lại không dao động nữa
A 0 = 3 Δ l 0 4 A 0 − 2 Δ l 0 + 4 A 0 − Δ l 0 = 3 S → S = 4 3 A 0
Kết hợp với x A 0 2 + v ω A 0 2 = 1 → A 0 = 9 S = 12 c m