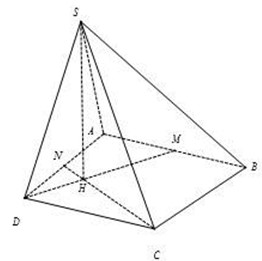
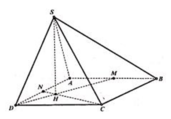
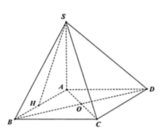
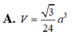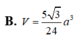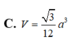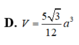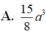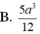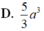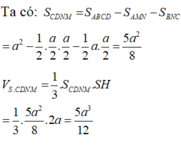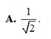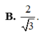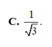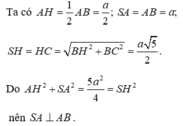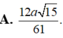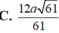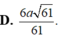Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB=2BC=2a. Gọi H là trung điểm của AB, SH vuông góc (ABCD). Gọi M là trung điểm của SH. Cạnh bên tạo với đáy (ABCD) góc 45 độ. Tính thể tích S.MCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 3 2017
Đáp án B
Ta có S C D N M = S A B C D - S A M N - S B N C
⇒ V S . C D N M = 1 3 . S C D N M . S H = 5 a 2 12
CM
6 tháng 5 2018
Đáp án: C
Hướng dẫn giải:
Ta có: H D = H A 2 + A D 2 = 2 a
Ta có: S A B C D = A B . B C = 2 a 2 3
⇒ V S . A B C D = 1 3 S H . S A B C D = 4 a 3
CM
28 tháng 11 2019
Vì S H ⊥ A B C D nên
V S . C D M N = 1 3 S H . S . C D M N = 1 3 S H . S A B C D - S B C M - S A M N = 1 3 a 3 5 8 a 2 = 5 3 24 a 3
Đáp án B
CM
28 tháng 9 2019
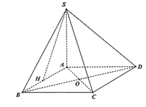
Ta có
A H = 1 2 A B = a 2 ; S A = A B = a S H = H C = B H 2 + B C 2 = a 5 2
Do A H 2 + S A 2 = 5 a 2 4 = S H 2 nên S A ⊥ A B
Do đó S A ⊥ A B C D nên S C , A B C D ^ = S C A ^
Trong tam giác vuông SAC có tan α = tan S C A ^ = S A A C = 1 2
Đáp án A
CM
1 tháng 6 2017
Đáp án C
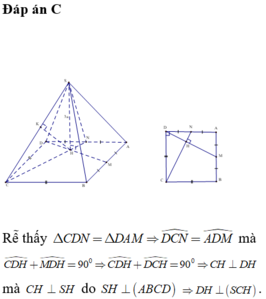
Rễ thấy Δ C D N = Δ D A M ⇒ D C N ^ = A D M ^
mà C D H ^ + M D H ^ = 90 0 ⇒ C D H ^ + D C H ^ = 90 0 ⇒ C H ⊥ D H
mà C H ⊥ S H do S H ⊥ A B C D ⇒ D H ⊥ S C H .
Như vậy kẻ H K ⊥ S C thì HK là đường vuông góc chung của DM và SC hay HK là khoảng cách cần xác định.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
C D 2 = C H . C N ⇒ C H = C D 2 C N = C D 2 C D 2 + D N 2 = 4 a 2 4 a 2 + a 2 = 2 a 5
1 H K 2 = 1 S H 2 + 1 C H 2 = 1 9 a 2 + 5 16 s 2 = 61 144 a 2 ⇒ H K = 12 a 61 61