cho tam giác abc có i, j lần lượt là trung điểm các cạnh ab, bc và
và IJ//BC
CMR: IJ=1/2BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 11 2015
Ta co:IA =IB(gt) ; HA =HC(gt)
Suy ra:HI la` đg tb của tam giac ABC
Suy ra:IH =1/2BC ;IH//BC (1)
Trong tam giac BDC co:KD =KB(gt) ;JD =JC(gt)
Suy ra :KJ la đg tb cu`a tam giac BDC
Suy ra :KJ =1/2BC ;KJ//BC (2)
Tu (1) va (2) suy ra :KJ = IH ;KJ // IH
Suy ra :tu giac KIHJ la hinh binh hanh(2 canh doi song song va bang nhau)(*)
Trong tam giac ADC co:HA =HC(gt) ;JD = JC(gt)
Suy ra :HJ la đg tb của tam giac ADC
Suy ra :HJ = 1/2AD
Mà AD =BC(gt) ; HI = 1/2BC(c/m tren)
Suy ra :HJ = HI (**)
Tu (*) va (**) suy ra tu giac KIHJ la hinh thoi (hbh co 2 canh ke bang nhau)
Suy ra :IJ vuong goc voi KH . . . . A B C D K H I J
21 tháng 9 2023
Tham khảo:
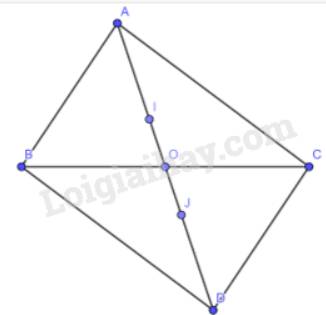
Vì I là trọng tâm tam giác ABC theo giả thiết nên ta có
\(AI = \dfrac{2}{3}AO = 2IO\)(định lí về trọng tâm trong tam giác)
Tương tự J là trọng tâm tam giác BCD nên ta có :
\(DJ = \dfrac{2}{3}OD = 2OJ\) (định lí về trọng tâm trong tam giác)
Mà OA = OD (giả thiết)
\( \Rightarrow AI = DJ = \dfrac{2}{3}OA = \dfrac{2}{3}OD = 2OI = 2OJ\)
Mà OI = OJ do cùng \( = \dfrac{1}{3}OA = \dfrac{1}{3}OD\)(tính chất trọng tâm trong tam giác)
\( \Rightarrow 2OI = 2OJ = 2\dfrac{1}{3}AO = 2\dfrac{1}{3}OD = IJ\)
\( \Rightarrow AI = DJ = IJ = \dfrac{2}{3}OA = \dfrac{2}{3}OD\)(điều phải chứng minh)
A
19 tháng 5 2020
Ta có: IJ−→=IA−→+AB−→−+BJ−→IJ→=IA→+AB→+BJ→
IJ−→=ID−→+DC−→−+CJ−→IJ→=ID→+DC→+CJ→
⇒IJ−→=12(AB−→−+DC−→−)⇒IJ→=12(AB→+DC→)
Xét:
HK−→−.IJ→=12(OK−→−−OH−→−).(AB−→−+DC−→−)=12(OK−→−.AB−→−+OK−→−.DC−→−−OH−→−.AB−→−−OH−→−.DC−→−)=12(OK−→−.AB−→−−OH−→−.DC−→−)=12[(OC−→−+CK−→−).(OB−→−−OA−→−)−(OA−→−+AH−→−).(OC−→−−OD−→−)]=12[(OB−→−−OA−→−−AH−→−).OC−→−−(CK−→−+OC−→−−OD−→−).OA−→−]=12[(HA−→−+AO−→−+OB−→−).OC−→−−(DO−→−+OC−→−+CK−→−).OA−→−]=12(HB−→−.OC−→−−DK−→−.OA−→−)=0⇔HK⊥IJ