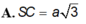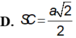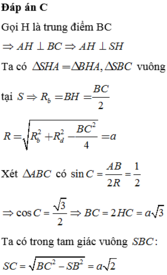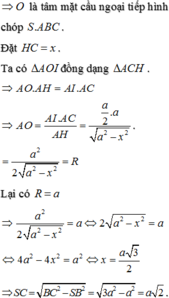HELP ME!!!!!
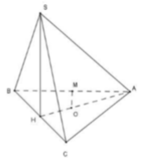
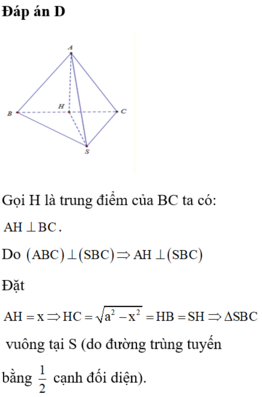
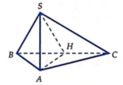
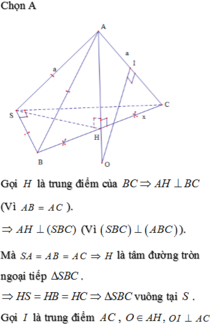
1> Cho hình chóp S.ABC có đáy là tam giác cân, AB = AC = a, (SBC) vuông góc với (ABC) và SA = SB =a. Cmr ∆ SBC vuông. Biết SC= x, tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC
2> Cho lăng trụ đứng tam giác ABC.A’B’C’ biết AA’ = AB = a, AC = 2a và góc BAC = 60⁰. Gọi M = A’C ∩ AC’. Tính thể tích tứ diện MBB’C và tính bán kính mặt cầu ngoại tiếp hình lăng trụ.