Cho tam giác DEF có góc EDF= 90 độ. Vẽ DK vuông góc EF tại K. Từ k vẽ KI vuông góc ED tại I.
a/ Cm góc EKI = IDK
b/ Cm góc KED=KDF
Giúp mình nha, cho mình xin cái hình lun. Mơn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
3 tháng 2 2022
Đúng(0)
Những câu hỏi liên quan
3 tháng 2 2022
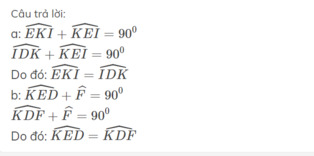
a: \(\widehat{EKI}+\widehat{KEI}=90^0\)
\(\widehat{IDK}+\widehat{KEI}=90^0\)
Do đó: \(\widehat{EKI}=\widehat{IDK}\)
b: \(\widehat{KED}+\widehat{F}=90^0\)
\(\widehat{KDF}+\widehat{F}=90^0\)
Do đó: \(\widehat{KED}=\widehat{KDF}\)
12 tháng 2 2022
a: \(\widehat{HAC}+\widehat{C}=90^0\)
\(\widehat{EHC}+\widehat{C}=90^0\)
Do đó: \(\widehat{HAC}=\widehat{EHC}\)
b: \(\widehat{BAH}+\widehat{B}=90^0\)
\(\widehat{ACH}+\widehat{B}=90^0\)
Do đó: \(\widehat{BAH}=\widehat{ACH}\)
26 tháng 4 2016
a) BD; CE là đường cao => tam giác ABD và tam giác ACE vuông : có: AB = AC (do tam giác ABC cân tại A ); góc A chung
=> tam giác ABD = ACE (cạnh huyền - góc nhọn )
b) Tam giác BDC vuông tại D có trung tuyến DH ứng với cạnh huyền BC => DH = HC = BC/ 2
=> tam giác HDC cân tại H
c) sửa đề: chứng minh: DM = MC
Tam giác DHC cân tại H có HM là đuơng cao nên đông thời là đường trung tuyến => M là TĐ của DC=> DM = MC
d) Tam giác HND vuông tại M có: MI là trung tuyến => MI = HI = HD/2
=> tam giác IHM cân tại I => góc IHM = IMH
lại có HM là p/g của góc DHC => góc IHM = MHC
=> góc IMH = MHC mà 2 góc này ở vị trí SLT => MI // HC mà HC vuông góc với AH
=> MI vuông góc với AH
28 tháng 4 2016
bạn Nobita Kun giải bài không theo điểm như đề bài cho, ý c đề bài đúng rồi ạ. ý d thì bạn hiểu nhầm đề rồi, bạn xem lại điểm I nhé
22 tháng 6 2023
a: Xét ΔEDC vuông tại D và ΔEHC vuông tại H có
EC chung
góc DEC=góc HEC
=>ΔEDC=ΔEHC
b: Xét ΔCDK vuông tại D và ΔCHF vuông tại H có
CD=CH
góc DCK=góc HCF
=>ΔCDK=ΔCHF
=>CK=CF
=>ΔCKF cân tại C