Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC.Gọi D là điểm đối xứng vs M qua AB. Gọi E là điểm đối xứng vs M qua AC. Chứng minh: a. điểm D đối xứng vs E qua A b.BD song song vs CE c. điểm M ở vị trí nào trên BC thì đoạn DE có độ dài nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 8 2022
Bổ sung đề; AM vuông góc BC
a: Ta có: M và D đối xứng nhau qua AB
nên AM=AD
=>ΔAMD cân tại A
=>AB là phân giác của góc MAD(1)
Ta có: M và E đối xứng nhau qua AC
nên AM=AE
=>ΔAME cân tại A
=>AC là phân giác của góc MAE(2)
Từ (1) và (2) suy ra góc DAE=2x90=180 độ
=>D,A,E thẳng hàng
mà AD=AE
nên A là trung điểm của DE
b: Xét ΔAMB và ΔADB có
AM=AD
MB=DB
AB chung
Do đó: ΔAMB=ΔADB
Suy ra: góc ADB=90 độ
hay BD vuông góc với DE(3)
Xét ΔAMC và ΔAEC có
AM=AE
MC=EC
AC chung
Do đó: ΔAMC=ΔAEC
Suy ra: góc AEC=90 độ
=>CE vuông góc với ED(4)
Từ (3) và (4) suy ra BD//CE
24 tháng 10 2021
a: Xét ΔABC có
D là trung điểm của BC
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔBAC
Suy ra: DE//AB
hay DE⊥AC
23 tháng 6 2021
Câu trả lời này ko phải của mik mà là của một bạn đã trả lời của bài toán này vào năm 2019. Nhớ vote mik nhé ^^
CH
Cô Hoàng Huyền
Admin
VIP
26 tháng 2 2018
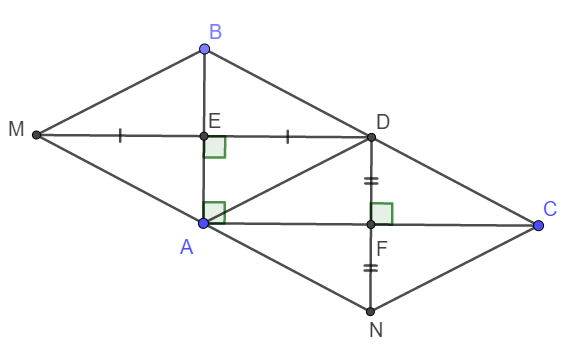
a) Tứ giác AEDF có 3 góc vuông nên AEDF là hình chữ nhật.
b) Do D là trung điểm BC nên E, F lần lượt là trung điểm của AB và AC.
Xét tứ giác ADBM có hai đường chéo cắt nhau tại trung điểm mỗi đường nên nó là hình bình hành.
Lại có \(AB\perp MD\) nên ADBM là hình thoi.
Tương tự ADCN cũng là hình thoi.
c) Ta có AB và AC lần lượt là phân giác của góc MAD và NAD
Vậy nên \(\widehat{MAN}=\widehat{MAD}+\widehat{NAD}=2\left(\widehat{BAD}+\widehat{FAD}\right)=180^o\)
Vậy M, A, N thẳng hàng.
Lại có AM = AD = AN nên A là trung điểm MN.
Hay M, N đối xứng nhau qua A.
d) Để hình chữ nhật AEDF trở thành hình vuông nên AE = AF hay AB = AC.
Vậy để AEDF là hình vuông thì tam giác ABC phải là tam giác vuông cân tại A.
12 tháng 11 2016
a) Tứ giác AEDF là hình chữ nhật
b) Tam giác ABC có BD = DC
DE//AC nên AE = BE
ta có DE =EM ( D đối xứng với M qua AB)Tứ giác ADBM có hai đường chéo cắt nhau tại trung điểm của mỗi dđường nện tứ giác ADBM là hình bình hành.
Tứ giác ADBM là hinh bình hành có hai đường chéo vuông góc AB vuông góc DM nên tứ giác ADBM là hình thoi
a/ Nối AM
- Do D đối xứng với M qua AB => AB là đường trung trực của MD
=> AD=AM (t/c đường trung trực)
- Do E đối xứng với M qua AC => AC là đường trung trực của ME
=> AE=AM (t/c đường trung trực)
Từ đó suy ra: AD=AE hay A là trung điểm của DE hay D đối xứng với E qua A (đpcm)
b/ Ta có: AM=AE (cmt)
- Tứ giác MAEC có: AE=AM => Tứ giác MAEC là hình thoi => CE // AM
Tương tự ta cũng có: AM=AD (cmt)
- Tứ giác ADBM có: AM=AD => Tứ giác ADBM là hình thoi => BD // AM
Từ đó suy ra được: BD // CE (đpcm)
c/ Điểm M phải là trung điểm của BC thì DE mới có độ dài nhỏ nhất