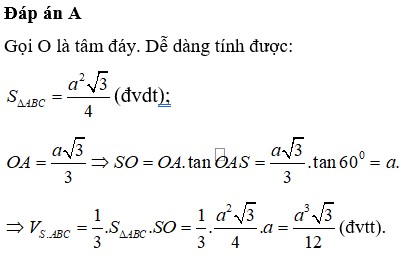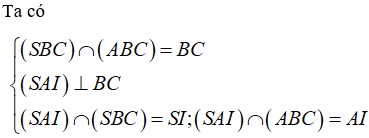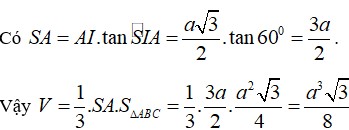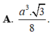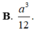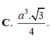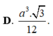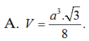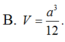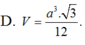cho hinh chóp đều SABC đường cao SO vuông góc với đáy canh bên bằng b góc giữa mặt bên và mặt đáy bằng 60 độ.tính thể tích SABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 11 2021
\(\widehat{SBA}=60^0\Rightarrow SA=AB.tan60^0=2a\sqrt{3}\)
\(\Rightarrow V=\dfrac{1}{3}SA.S_{ABC}=\dfrac{1}{3}.2a\sqrt{3}.\dfrac{\left(2a\right)^2\sqrt{3}}{4}=2a^3\)

AH
Akai Haruma
Giáo viên
11 tháng 3 2021
Lời giải:
$H$ là chân đường cao của hình chóp đều nên $H$ chính là tâm đường tròn ngoại tiếp tam giác $ABC$
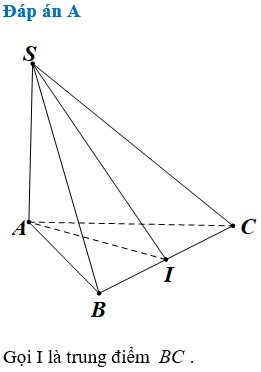
Kẻ $HM\perp BC$. Dễ thấy $M$ là trung điểm $BC$ và $SBC$ cân tại $S$ nên $SM\perp BC$
Do đó:
$\angle ((SBC), (ABC))=\angle (SM, HM)$
$=\widehat{SMH}=60^0$
$\frac{SH}{HM}=\tan \widehat{SMH}=\tan 60^0=\sqrt{3}$
$\Rightarrow SH=\sqrt{3}HM$
Mà: $HM=\frac{1}{3}AM=\frac{1}{3}.\sqrt{AB^2-BM^2}=\frac{1}{3}\sqrt{AB^2-(\frac{BC}{2})^2}=\frac{\sqrt{3}}{6}a$
Do đó: $SH=\sqrt{3}HM=\frac{3}{6}a=\frac{1}{2}a$