Mn cho em hỏi đây là lý thuyết nào vậy ạ
Cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác, D là điểm đối xứng của A qua O.
Vì AD là đường kính của đường tròn tâm O nên BD⊥AB,DC⊥AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 3 2018
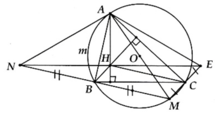
a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3
30 tháng 4 2020
a . Gọi AH ∩ BC=D,BH ∩ AC=E,CH ∩ AB=F
\(\Rightarrow AD\perp BC,BE\perp AC,CF\perp AB\)
\(\Rightarrow\widehat{ADC}=\widehat{AFC}=90^0\) => ◊AFDC nội tiếp
\(\Rightarrow\widehat{DCF}=\widehat{DAF}\)
VÌ H đối xứng H' qua BC
\(\Rightarrow HH'\perp BC\Rightarrow A,H,,D,H'\)thẳng hàng
\(\Rightarrow\widehat{BAH'}=\widehat{DAF}=\widehat{FDC}=\widehat{HCB}\)
Lại có: H đối xứng với H' qua BC
\(\Rightarrow\widehat{BCH'}=\widehat{HCB}\)
\(\Rightarrow\widehat{BCH'}=\widehat{BAH'}\Rightarrow\)
\(\Rightarrow BC\perp AA'\Rightarrow A,H,D,H',A'\) thẳng hàng
Vì \(H,H'\) đối xứng qua BC , A,A' đối xứng qua BC
\(\Rightarrow\widehat{BHC}=\widehat{BH'C},\widehat{BAC}=\widehat{BA'C}\)
Lại có ◊ ABH'C nội tiếp
\(\Rightarrow\widehat{BAC}+\widehat{BH'C}=180^0\)
\(\Rightarrow\widehat{BA'C}+\widehat{BHC}=180^0\)
=> ◊ BHCA' nội tiếp
=> Bán kính đường tròn ngoại tiếp \(\Delta BHC\) bằng bán kính đường tròn ngoại tiếp \(\Delta A'BC\)
Ta có : A , A' đối cứng qua BC
\(\Rightarrow A'B=AB,CA=CA'\Rightarrow\Delta ABC=\Delta A'BC\left(c.c.c\right)\)
=> Bán kính đường tròn ngoại tiếp \(\Delta A'BC\) bằng bán kính đường tròn ngoại tiếp ΔABC
=> Bán kính đường tròn ngoại tiếp \(\Delta BHC\) bằng bán kính đường tròn ngoại tiếp ΔABC
DD
Đoàn Đức Hà
Giáo viên
24 tháng 5 2022
a) Ta có: \(\widehat{AMO}=\widehat{ADO}=\widehat{ANO}=90^o\) nên \(M,N,D\) cùng nhìn \(AO\) dưới một góc vuông suy ra \(M,D,O,N,A\) cùng thuộc một đường tròn.
b) Gọi \(F\) là giao điểm của \(AC\) và đường tròn \(\left(O\right)\).
\(\Delta ANF\sim\Delta ACN\left(g.g\right)\) suy ra \(AN^2=AC.AF\).
Xét tam giác \(AHN\) và tam giác \(AND\):
\(\widehat{HAN}=\widehat{NAD}\) (góc chung)
\(\widehat{ANH}=\widehat{ADN}\) (vì \(AMDON\) nội tiếp, \(\widehat{ANH},\widehat{ADN}\) chắn hai cung \(\stackrel\frown{AM},\stackrel\frown{AN}\) mà \(AM=AN\))
\(\Rightarrow\Delta AHN\sim\Delta AND\left(g.g\right)\)
suy ra \(AN^2=AH.AD\)
suy ra \(AC.AF=AH.AD\)
\(\Rightarrow\Delta AFH\sim\Delta ADC\left(c.g.c\right)\Rightarrow\widehat{AFH}=\widehat{ADC}=90^o\)
suy ra \(\widehat{HFC}=90^o\) mà \(\widehat{BFC}=90^o\) (do \(F\) thuộc đường tròn \(\left(O\right)\))
suy ra \(B,H,F\) thẳng hàng do đó \(BH\) vuông góc với \(AC\).
Tam giác \(ABC\) có hai đường cao \(AD,BF\) cắt nhau tại \(H\) suy ra \(H\) là trực tâm tam giác \(ABC\).
Góc nội tiếp chắn nửa đường tròn là góc vuông
kiến thức lớp mấy vậy ạ