giúp mình 2 câu này nha 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: 1436<x<1440
=> x ={1437; 1438 ; 1439}
Mà x chia hết cho 2
=> x= 1438
Vậy x= 1438

22.
\(a,f\left(2\right)=2^2-5.2+6=4-10+6=0\\ f\left(-0,75\right)=\left(-0,75\right)^2-5\left(-0,75\right)+6=\dfrac{9}{16}+\dfrac{15}{4}+6=\dfrac{165}{16}\)
\(b,\text{để y=6 thì}x^2-5x+6=6\\ \Leftrightarrow x^2-5x=0\\ \Leftrightarrow x\left(x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)

Về phương diện tính từ hay danh từ ạ ??

\(\dfrac{2}{x-3}+\dfrac{x-5}{x-1}=1.\left(x\ne3;1\right).\\ \Leftrightarrow\dfrac{2x-2+\left(x-5\right)\left(x-3\right)-\left(x-3\right)\left(x-1\right)}{\left(x-3\right)\left(x-1\right)}=0.\\ \Rightarrow2x-2+x^2-3x-5x+15-x^2+4x-3=0.\\ \Leftrightarrow-2x+10=0.\\ \Leftrightarrow x=5.\)

`3/4-(2/3+3/4)+2/3+2022/2023`
`=3/4 - 2/3 - 3/4 +2/3 +2022/2023`
`= (3/4 -3/4 ) + (-2/3 +2/3) +2022/2023`
`= 0+0+2022/2023`
`=2022/2023`
\(\dfrac{3}{4}-\left(\dfrac{2}{3}+\dfrac{3}{4}\right)+\dfrac{2}{3}+\dfrac{2022}{2023}\)
\(=\dfrac{3}{4}-\left(\dfrac{8}{12}+\dfrac{9}{12}\right)+\dfrac{2}{3}+\dfrac{2022}{2023}\)
\(=\dfrac{3}{4}-\dfrac{17}{12}+\dfrac{2}{3}+\dfrac{2022}{2023}\)
\(=\dfrac{9}{12}-\dfrac{17}{12}+\dfrac{8}{12}+\dfrac{2022}{2023}\)
\(=\dfrac{9-17+8}{12}+\dfrac{2022}{2023}=\dfrac{0}{12}+\dfrac{2022}{2023}=0+\dfrac{2022}{2023}\)
\(=\dfrac{2022}{2023}\)
#YTVA

\(A=2+2^3+...+2^{2009}\)
\(2^2.A=2^3+2^5+...+2^{2011}\)
\(4A-A=\left(2^3+2^5+...+2^{2011}\right)-\left(2+2^3+...+2^{2009}\right)\)
\(3A=2^{2011}-2\)
\(\Rightarrow A=\frac{2^{2011}-2}{3}\)

a) Xét tam giác ABD và tam giác EBD có:
AB = EB (gt).
^ABD = ^EBD (BD là phân giác).
BD chung.
=> Tam giác ABD = tam giác EBD (c - g - c).
=> DA = DE (cặp cạnh tương ứng).
b) Tam giác ABD = tam giác EBD (cmt).
=> ^BAD = ^BED (cặp góc tương ứng).
Mà ^BAD = 90 độ (tam giác ABC vuông tại A).
=> ^BED = 90 độ.
c) Xét tam giác KBC có:
CA là đường cao (^CAB = 90 độ).
KE là đường cao (^KEC = 90 độ).
Mà D là giao điểm của CA và KE.
=> D là trực tâm của tam giác KBC.
=> BD là đường cao.
=> BD vuông góc KC. (1)
Xét tam giác KBC có:
BD là đường cao (cmt).
BD là phân giác góc KBC (gt).
=> Tam giác KBC cân tại B.
Xét tam giác ABE có:
BE = BA (gt).
=> Tam giác ABE cân tại B.
Xét tam giác ABE cân tại B có:
BD là phân giác góc ABE (gt).
=> BD là đường cao (tính chất các đường trong tam giác cân).
=> BD vuông góc AE. (2)
Từ (1); (2) => AE // KC ( từ vuông góc đến song song).

a) Xét tam giác ABM và tam giác CDM có:
+ BM = DM (M là trung điểm BD).
+ ^AMB = ^CMD (đối đỉnh).
+ AM = CM (M là trung điểm AC).
=> Tam giác ABM = Tam giác CDM (c - g - c).
b) Vì tam giác ABM = tam giác CDM (cmt).
=> AB = CD (2 cạnh tương ứng).
Ta có: ^BAM = 90o (Tam giác ABC vuông tại A).
Mà ^BAM = ^DCM (tam giác ABM = tam giác CDM).
=> ^BAM = ^DCM = 90o.
=> CD vuông góc AC (đpcm).
c) Ta có: AB = CD (cmt).
Mà CD = CE (gt).
Xét tứ giác ACEB có:
+ AB = CE (cmt).
+ AB // AC (do cùng vuông óc với AC).
=> Tứ giác ADEB là hình bình hành (dhnb).
=> Giao điểm của 2 đường chéo BC và AE là trung điểm của mỗi đường (Tính chất hình bình hành).
Mà O là trung điểm của BC (gt).
=> O là trung điểm của AE.
=> 3 điểm A; O; E thẳng hàng (đpcm).
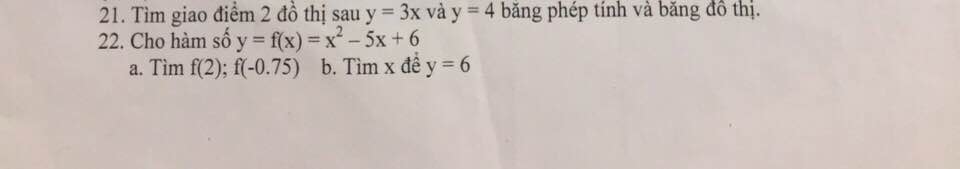
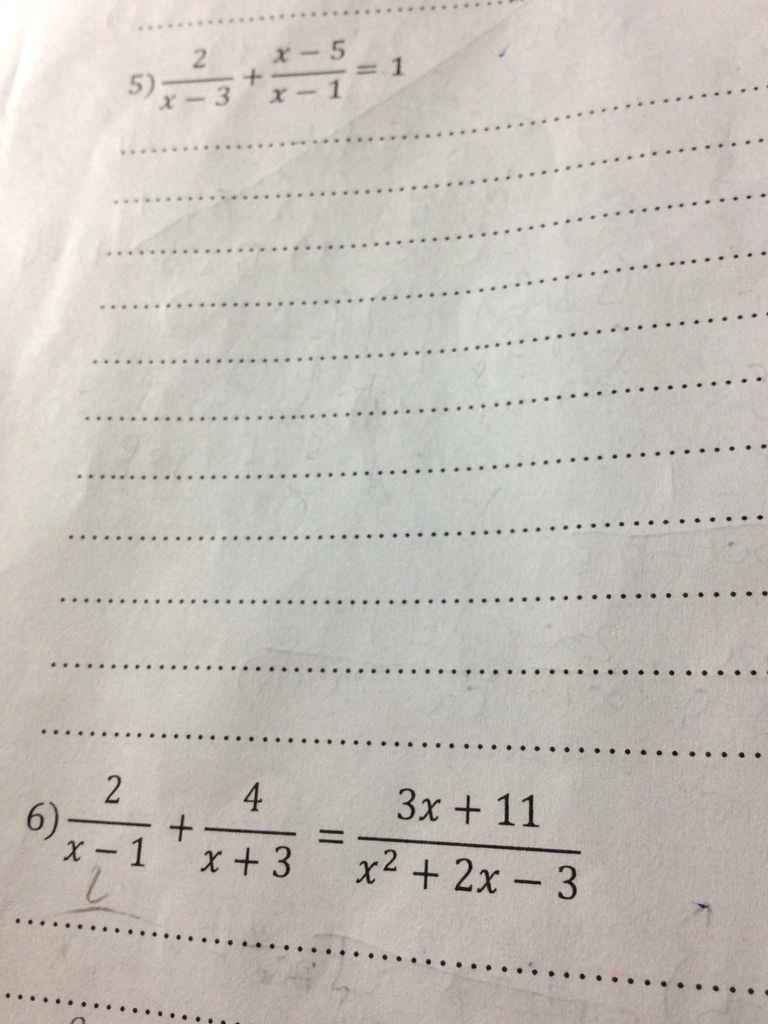 Giúp mình thêm 2 câu này cực gấp luôn nha cảm ơn
Giúp mình thêm 2 câu này cực gấp luôn nha cảm ơn
13. \(A=\left\{0\right\}\)
14. Có vô hạn số tự nhiên không vượt quá n trong đó n thuộc N*
13.A={0} .
14.Có n số tự nhiên không vượt quá n .