Một con lắc dơn có chiều dài \(l\), dao động điều hòa tại một nơi có gia tốc rơi tự do \(g\) với biên độ góc α0. Lúc vật đi qua vị trí có li độ góc α, nó có vận tốc là \(v\). Biểu thức nào sau đây là đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án B
+ Tần số dao động con lắc đơn: f = ω 2 π = 1 2 π g l

Do \(\alpha_0=8^0\) nên đây là dao động điều hòa, ta tính toán giống như một dao động điều hòa thôi.
Tại vị trí \(W_đ=W_t\)
\(\Rightarrow W=W_đ+W_t=2W_đ\)
\(\Rightarrow v_{max}^2=2.v^2\)
\(\Rightarrow v=\dfrac{v_{max}}{\sqrt 2}=\dfrac{\omega.A}{\sqrt 2}\)
\(\Rightarrow v=\dfrac{\sqrt{\dfrac{g}{\ell}}.\alpha_0.\ell}{\sqrt 2}=\dfrac{\alpha_0.\sqrt{g.\ell}}{\sqrt 2}\)
\(\Rightarrow v=\dfrac{\dfrac{8.\pi}{180}.\sqrt{10.1}}{\sqrt 2}\approx0,31(m/s)\)

Đáp án A
Vị trí có li độ x = 2 2 A vật có E d = E t = 0 , 5 E = 0 , 25 m ω 2 A 2 .


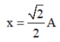

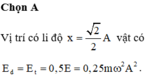
Bạn áp dụng CT của dao động điều hòa:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\)
Với \(x=\alpha.\ell\), li độ là độ dài cung của góc \(\alpha\) (tính theo rad)
\(\Rightarrow (\alpha_0.\ell)^2=(\alpha.\ell)^2+\dfrac{v^2.\ell}{g}\)
\(\Rightarrow \alpha_0^2=\alpha^2+\dfrac{v^2}{g\ell}\)
Chọn đáp án A.
Cảm ơn bạn