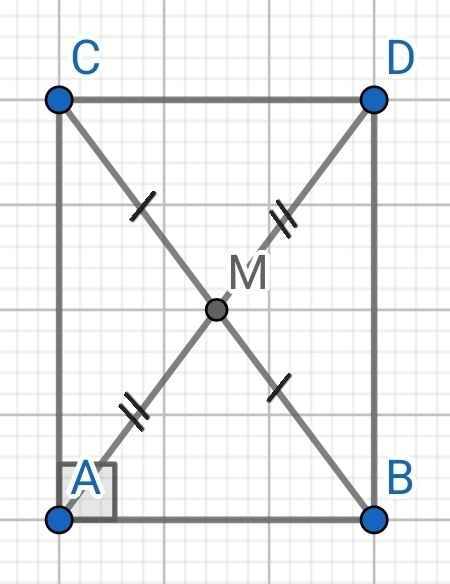
Cho tam giác ABC vuông tại A. Điểm M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD. Chứng minh rằng:1/ ∆AMC = ∆DMB. 2/ AC = BD.3/ AB vuông góc với BD. 4/ AM = ½...
Đọc tiếp
Cho tam giác ABC vuông tại A. Điểm M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD. Chứng minh rằng:
1/ ∆AMC = ∆DMB. 2/ AC = BD.
3/ AB vuông góc với BD. 4/ AM = ½ BC.
1) vì M là trung điểmcủa BC nên MB=MC
do MA=MD và 2 góc AMC=BMD (đối đỉnh)
vậy 2tam giácAMC=BMD ( c,g,c)
2) do 2tam giác AMC=BMD nên AB=BD (2canh tương ứng)
3) dohình bình hành ACDB có 2 đường céo AD=BC và cắt nhau tại trung điểm của mỗi đường
và có góc vuông tại A => ACDB là hình chữ nhật => AB vuông góc BD
4) M là trung điểm BC => AM là trung tuyến tam giác ABC=> AM= 1/2 BC
sao hk vẽ hih
`