Một vật dao động điều hòa với phương trình 
. Tìm thời điểm vật qua vị trí có li độ x = +5 cm lần thứ 2 theo chiều dương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 8 2016
\(t=0,4s\)
\(t=0\Rightarrow x=10=A\)
Thời điểm vật qua vị trí \(x=5=\frac{A}{2}\)
Vì trong một chu kỳ vật đi qua vị trí x=5 lần nên :
\(t=\frac{2008}{2}=1003.2+2=1003T+t'\)
Vẽ trục ngang ra tìm t'\(\Rightarrow t'=\frac{T}{2}+\frac{T}{4}+\frac{T}{12}\)Vậy : t' = 2003T + 5T/6 = 6023T/6 = 401,53 (s)
VT
1 tháng 1 2018
Đáp án A
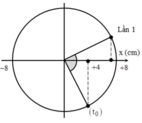
+ Tại thời điểm t = 0 vật đi qua vị trí x = 4 cm theo chiều dương.
Trong mỗi chu kì vật đi qua vị trí x = 4 3 cm theo chiều âm 1 lần → Ta tách 2017 = 2016 + 1.
+ Biểu diễn các vị trị tương ứng trên đường tròn, từ hình vẽ. Ta có:
Δt = 2016T + 0,25T = 2016,25 s
VT
16 tháng 11 2019
Chọn C
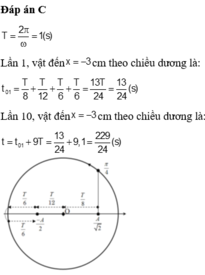
+ Chu kỳ dao động T = 0,2 (s)
+ t = 0: x=10 cos0 = 10cm = +A.
+ Thời gian vật đi từ vị trí ban đầu x = +A tới x = 5cm = A/2 chuyển động theo chiều dương lần thứ nhất là:
t1 = tA→-A + t-A→O + tO→A/2
+ Còn 2008 lần sau đó, cứ một chu kì vật lại qua x = A/2 theo chiều dương một lần nên cần thời gian 2008T.
+ Thời điểm vật đi qua vị trí li độ x = 5cm lần thứ 2009 theo chiều dương:
t = t1 + 2008T = 401,76 s.
VT
3 tháng 9 2017
Đáp án A
Tại thời điểm t = 0 vật đi qua vị trí x = 4cm theo chiều dương
+ Trong mỗi chu kì vật đi qua vị trí x = 4 3 c m 1 lần → Ta tách 2017 = 2016 + 1
+ Biểu diễn các vị trí trên đường tròn, từ hình vẽ. Ta có:
△ t = 2016T + 0,25t = 2016,25s
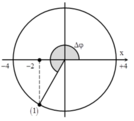
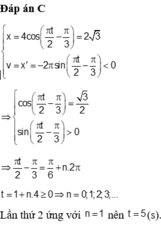
Vẽ vòng tròn véc tơ quay ta có:
Ban đầu, véc tơ quay xuất phát ở M, quay ngược chiều kim đồng hồ.
Vật qua li độ x = +5cm khi véc tơ quay đến N.
Để qua lần thứ 2 thì véc tơ quay phải quay như hình vẽ.
Thời gian là: \(t=T+\dfrac{T}{2}+\dfrac{30}{360}T=\dfrac{19}{12}T=\dfrac{19}{12}.1=\dfrac{19}{12}(s)\)