Cho Δ ABC có góc A = 90 độ , từ B , C vẽ hai tia Bx , Cy cùng nằm ở \(\frac{1}{2}\) mặt phẳng bờ BC chứa điểm A và vuông góc với BC . Tính góc xBA + góc yCA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 9 2016
Từ A kẻ tia AA' nằm trong góc BAC và vuông góc với BC
Do Bx; Cy; AA' đều vuông góc với BC => Bx // Cy // AA'
Ta có: góc ACy = góc CAA' (so le trong)
góc A'AB = góc ABx (so le trong)
=> góc ACy + góc ABx = góc CAA' + góc A'AB
Lại có: góc CAA' + góc A'AB = 90o
=> góc ACy + góc ABx = 90o
15 tháng 7 2015
Bài của thang Tran nè :
Bx vuông góc với BC , Cy vuông góc cới BC => CBx= 90 độ ; BCy = 90 độ
CBx = ABx + ABC = 90 độ (1)
BCy = ACB + ACy = 90 độ (2)
Từ (1) và (2) => ABx+ ABC + ACB + ACY = 90 + 90 = 180 độ (3)
TAm giác ABC có A = 90 độ => ABC +ACB = 90 độ thay vào (3) ta có:
ABx + ACy + 90 độ = 180 độ
=> ABx + ACy = 18 0 - 90 = 90o
19 tháng 9 2018
Bx vuông góc với BC , Cy vuông góc cới BC => CBx= 90 độ ; BCy = 90 độ
CBx = ABx + ABC = 90 độ (1)
BCy = ACB + ACy = 90 độ (2)
Từ (1) và (2) => ABx+ ABC + ACB + ACY = 90 + 90 = 180 độ (3)
TAm giác ABC có A = 90 độ => ABC +ACB = 90 độ thay vào (3) ta có:
ABx + ACy + 90 độ = 180 độ
=> ABx + ACy = 18 0 - 90 = 90
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 1 2022
1c (2 câu kia em tự giải)
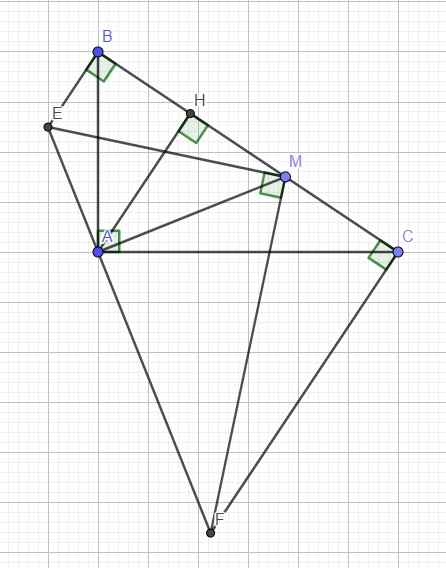
Kẻ đường cao AH \(\Rightarrow\) AH cố định
Do \(\widehat{MAF}\) và \(\widehat{MCF}\) cùng nhìn MF dưới 1 góc vuông nên tứ giác MAFC nội tiếp
\(\Rightarrow\widehat{AFM}=\widehat{ACM}\) (cùng chắn AM)
\(\Rightarrow\Delta_VFME\sim\Delta_VCAB\left(g.g\right)\) với tỉ số đồng dạng \(k=\dfrac{AM}{AH}\)
\(\Rightarrow S_{MEF}=k^2.S_{ABC}\Rightarrow S_{MEF-min}\) khi \(k_{min}\)
Mà trong tam giác vuông AHM ta có \(AH\le AM\Rightarrow k\ge1\Rightarrow k_{min}=1\) khi M trùng H
Hay diện tích MEF min khi M là chân đường cao từ A xuống BC
