Cho y = \(x^3-3mx^2+3m^3\) Tìm m để có 2 cực trị A,B thỏa mãn tam giác OAB có diện tích bằng 48.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2016
Với mọi \(x\in R,y'=3x^2+6mx\Rightarrow y'=0\Leftrightarrow x=0\) hoặc \(x=-2m\)
Để hàm số có cực đại, cực tiểu thì phương trình \(y'=0\) có 2 nghiệm phân biệt \(\Leftrightarrow m\ne0\). Khi đó, tọa độ các điểm cực trị là \(A\left(0;2\right),B\left(-2m;4m^3+2\right)\)
\(S_{OAB}=1\Leftrightarrow OA.d\left(B;OA\right)=4\Leftrightarrow\left|2\right|=2\Leftrightarrow\begin{cases}m=1\\m=-1\end{cases}\) (thỏa mãn)
Vậy với \(m=\pm1\) thì hàm số có 2 cực trị thỏa mãn bài
CM
18 tháng 2 2019
+ Đạo hàm y’ = 3x2- 6mx= 3x( x- 2m)
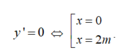
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi :m≠0. (1)
+ Tọa độ các điểm cực trị của đồ thị hàm số là A( 0 ; 3m3) ; B( 2m; -m3)
Ta có: O A → ( 0 ; 3 m 3 ) ⇒ O A = 3 m 3 ( 2 )
Ta thấy A ∈ O y ⇒ O A ≡ O y ⇒ d ( B ; O A ) = d ( B ; O y ) = 2 m (3)
+ Từ (2) và (3) suy ra S= ½. OA.d(B ; OA)=3m4.
Do đó: S ∆ O A B = 48 ⇔ 3 m 4 = 48 ⇔ m = ± 2 (thỏa mãn (1) ).
Chọn D.
CM
9 tháng 4 2017
Chọn D
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi
2m ≠ 0 ⇔ m ≠ 0 (1)
Khi đó, các điểm cực trị của đồ thị hàm số là
Ta có: O A ⇀ ( 0 ; 3 m 3 ) ⇒ O A = 3 m 3 (2)
Ta thấy A ∈ O y ⇒ O A ≡ O y
⇒ d ( B , O A ) = d ( B , O y ) = 2 m ( 3 )
Từ (2) và (3) suy ra
S ∆ O A B = 1 2 . O A . d ( B , O A ) = 3 m 4
Do đó: S ∆ O A B = 48 ⇔ m = ± 2 (thỏa mãn (1)
CM
8 tháng 12 2017
Chọn D
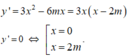
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi : 2m ≠ 0 ⇔ m ≠ 0 (1)
Khi đó, các điểm cực trị của đồ thị hàm số là
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
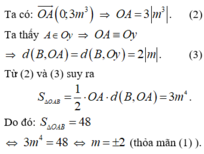
\(f'\left(x\right)=4x^3-4mx=4x\left(x^2-m\right)\)
Hàm có 3 cực trị khi \(m>0\Rightarrow\left[{}\begin{matrix}x=0;y=3m^2-m+2\\x=-\sqrt{m};y=2m^2-m+2\\x=\sqrt{m};y=2m^2-m+2\end{matrix}\right.\)
\(S_{ABC}=\dfrac{1}{2}\left|-\sqrt{m}-\sqrt{m}\right|.\left|\left(3m^2-m+2\right)-\left(2m^2-m+2\right)\right|\)
\(=\sqrt{m}.m^2=32\)
\(\Rightarrow\sqrt{m^5}=2^5\Rightarrow m=4\)
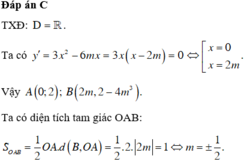
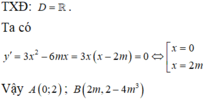
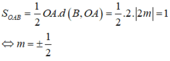
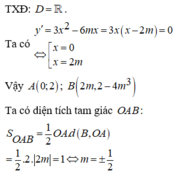
y' = 3x^2 - 6mx = 3x(x-2m)
với y'=0 <=> x=0 hoặc x-2m= 0
để hàm có 2 cực trị <=> x = 2m (m#0)
chứng tỏ với mọi m #0 thì hàm luôn có 2 điểm cực trị
giả sử 2 điểm cực trị là A ( 0 ; 3m^3 ) ; B ( 2m ; 0 )
=> OA = 3m^3 ; OB = 2m
diện tích OAB = 48 <=> 1/2 . OA.OB = 48 <=> 1/2. 3m^3 . 2m = 48 <=> 3m^3 = 48 <=> m =\(\sqrt[3]{16}\) (TM )
vậy ....