1)cho tam giac co 3 cạnh tỉ lệ với các số 3 4 5 và chu vi bằng 36 cm tinh do dai cac canh cua tam giac
2)Phân tích số 480 thành tổng 3 sốvaf 3 số đó tỉ lệ với 2 3 5 tìm 3 số đó
Cácbạn làm giúp mình nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
12 tháng 7 2016
Câu 1:
Gọi độ dài 3 cạnh của tam giác lần lượt là a,b,c
Vì chu vi tam giác bằng 36 cm
\(\Rightarrow\)a+b+c=36
Mà 3 cạnh của tam giác tỉ lệ với 3,4,5
\(\Rightarrow\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\Rightarrow\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)
\(\Rightarrow\)\(\frac{a}{3}=3;\frac{b}{4}=3;\frac{c}{5}=3\)
\(\Rightarrow\)a=9;b=12;c=15
Vậy ba cạnh của tam giác là 9;12;15
12 tháng 7 2016
Bài này làm đơn giản thế này thôi nhé Kia-K3 ^^
1) Gọi độ dài 3 cạnh của tam giác lần lượt là x, y, z
Ta có : \(\begin{cases}x+y+z=36\\\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\end{cases}\)
Áp dụng tính chất dãy tỉ số bằng nhau : \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{36}{12}=3\)
\(\Rightarrow\begin{cases}x=3.3=9\\y=4.3=12\\z=5.3=15\end{cases}\) .
2) Tương tự, ta cũng gọi các số đó là x,y,z
Theo đề bài : \(\begin{cases}x+y+z=480\\\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\end{cases}\)
Cũng áp dụng tính chất dãy tỉ số bằng nhau , ta được \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{2+3+5}=\frac{480}{10}=48\)
\(\Rightarrow\begin{cases}x=48.2=96\\y=48.3=144\\z=48.5=240\end{cases}\)
PA
17 tháng 7 2016
Bài 1:
Gọi 4 phần đó lần lượt là a, b, c, d.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{d}{9}=\frac{a+b+c+d}{3+5+7+9}=\frac{12}{24}=\frac{1}{2}\)
\(\frac{a}{3}=\frac{1}{2}\Rightarrow a=\frac{3}{2}\)
\(\frac{b}{5}=\frac{1}{2}\Rightarrow b=\frac{5}{2}\)
\(\frac{c}{7}=\frac{1}{2}\Rightarrow c=\frac{7}{2}\)
\(\frac{d}{9}=\frac{1}{2}\Rightarrow d=\frac{9}{2}\)
Bài 2:
Gọi 3 cạnh của tam giác lần lượt là a, b, c.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{40,5}{15}=2,7\)
\(\frac{a}{3}=2,7\Rightarrow a=2,7\times3=8,1\)
\(\frac{a}{5}=2,7\Rightarrow2,7\times5=13,5\)
\(\frac{c}{7}=2,7\Rightarrow c=2,7\times7=18,9\)
17 tháng 7 2016
Bài 1:
Gọi số 12 thành 4 phần lần lượt là:a,b,c,dvà a,b,c,d phải là số dương.
Ta có: \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{d}{9}\) và a+b+c+d=12
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{d}{9}=\frac{a+b+c+d}{3+5+7+9}=\frac{12}{24}=0,5\)
- \(\frac{a}{3}=0,5.3=1,5\)
- \(\frac{b}{5}=0,5.5=2,5\)
- \(\frac{c}{7}=0,5.7=3,5\)
- \(\frac{d}{9}=0,5.9=4,5\)
Vậy số 12 thành 4 phần lần lượt là: 1,5;2,5;3,5;4,5.
Bài 2:
Gọi mỗi cạnh của tam giác lần lượt là:x(cm),y(cm),z(cm) và x,y,z phải là số dương.
Ta có :\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\) và x+y+z=40,5
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{x+y+z}{3+5+7}=\frac{40,5}{15}=2,7\)
- \(\frac{x}{3}=2,7.3=8,1\)
- \(\frac{y}{5}=2,7.5=13,5\)
- \(\frac{z}{7}=2,7.7=18,9\)
Vậy mỗi cạnh của tam giác lần lượt là: 8,1;13,5;18,9.
^...^ 
^_^
5 tháng 10 2021
Bài 1:
Gọi 4 phần đó lần lượt là a, b, c, d.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{d}{9}=\frac{a+b+c+d}{3+5+7+9}=\frac{12}{24}=\frac{1}{2}\)
\(\frac{a}{3}=\frac{1}{2}\Rightarrow a=\frac{3}{2}\)
\(\frac{b}{5}=\frac{1}{2}=\Rightarrow b=\frac{5}{2}\)
\(\frac{c}{7}=\frac{1}{2}\Rightarrow c=\frac{7}{2}\)
\(\frac{d}{9}=\frac{1}{2}\Rightarrow d=\frac{9}{2}\)
Bài 2:
Gọi mỗi cạnh của tam giác lần lượt là:x (cm) , y (cm) , z (cm) và x , y , z phải là số dương.
Ta có : \(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\) và \(x+y+z=40,5\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{x+y+z}{3+5+7}=\frac{40,5}{15}=2,7\)
\(\frac{x}{3}=2,7.3=8,1\frac{y}{5}=2,7.5=13,5\frac{z}{7}=2,7.7=18,9\)
Vậy mỗi cạnh của tam giác lần lượt là: \(8,1;13,5;18,9\)
28 tháng 10 2018
Bài 1 :
Số đó chia hết cho 18 => chia hết cho 2 và 9
=> Số đó có tận cùng là chữ số chẵn và có tổng các chữ số chia hết cho 9
Chữ số có tận cùng chẵn nên chỉ có thể lớn nhất bằng 8 , mỗi chữ số còn lại lớn nhất bằng 9
=> Tổng các chữ số lớn nhất bằng 9 + 9 + 8 = 26
Gọi 3 chữ số đó là x , y , z là \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\)
+ ) Nếu x + y + z = 9
Ta có \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}=\frac{x+y+z}{1+2+3}=\frac{9}{6}=\frac{3}{2}\Rightarrow x=\frac{3}{2}\)( loại )
+) Nếu x + y + z = 18
\(\Rightarrow\frac{x}{1}=\frac{y}{2}=\frac{z}{3}=\frac{x+y+z}{1+2+3}=\frac{18}{6}=3\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{1}=3\\\frac{y}{2}=3\\\frac{z}{3}=3\end{cases}}\Rightarrow\hept{\begin{cases}x=3\\y=6\\z=9\end{cases}}\)
Vì số đó là số chẵn nên ta được 396 và 936
Bài 2 : Mình đã làm trên cho bạn rồi nhỉ ?
=> NHỚ TÍCH CHO MIK NHÉ !
18 tháng 10 2018
bn vào link này tham khảo bài 3 nhé
https://olm.vn/hoi-dap/tim-kiem?q=t%C3%ACm+%C4%91%E1%BB%99+d%C3%A0i+3+c%E1%BA%A1nh+c%E1%BB%A7a+tam+gi%C3%A1c+bi%E1%BA%BFt+chu+vi+b%E1%BA%B1ng+19+cm+v%C3%A0+%C4%91%E1%BB%99+d%C3%A0i+3+c%E1%BA%A1nh+t%E1%BB%89+l%E1%BB%87+ngh%E1%BB%8Bch+v%E1%BB%9Bi+c%C3%A1c+s%E1%BB%91+2;4;5+&id=925099
18 tháng 10 2018
bài 3.
Gọi đọ dài 3 cạnh của hình tam giác là: a;b;c.
Vì a;b;c tỉ lệ với 1,2 ; 1,3 ; 1,5 nên
\(\frac{a}{1,2}=\frac{b}{1,3}=\frac{c}{1,5}\)và\(a+b+c=36\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{1,2}=\frac{b}{1,3}=\frac{c}{1,5}=\frac{a+b+c}{1,2+1,3+1,5}=\frac{36}{4}=9\)
vì \(\frac{a}{1,2}=9\Rightarrow a=9\cdot1,2=10,8\)
vì \(\frac{b}{1,3}=9\Rightarrow b=11,7\)
vì \(\frac{c}{1,5}=9\Rightarrow c=13,5\)
vậy 3 cạnh của tam giác đó là 10,8cm;11,7cm;13,5cm
MẤY Ý TIẾP THEO TƯƠNG TỰ NHA
15 tháng 10 2016
Ta có: a + b + c = 36
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
a/3 = b/4 = c/5 = (a + b + c)/(3 + 4 + 5) = 36/12 = 3
Độ dài ba cạnh của tam giác vuông là:
a/3 = 3 => a = 9
b/4 = 3 => b = 12
c/5 = 3 => c = 15
Diện tích tam giác vuông đó là: 1/2 . a.b = 1/2 . 9. 12 = 54 (đvdt)
IM
15 tháng 10 2016
Gọi 3 cạnh của tam giác là a ; b ; c thỏa mãn \(\begin{cases}\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\\a+b+c=36\end{cases}\)
Áp dụng tc của dãy tỉ số bằng nhau ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)
\(\Rightarrow\begin{cases}a=9\\b=12\\c=15\end{cases}\)
Ta biết trong tam giác vuông , cạnh huyền là cạnh lớn nhất
=> 2 cạnh góc vuông là 9 và 12
\(\Rightarrow S=\frac{9.12}{2}=54\) ( đơn vị diện tích )
HN
6 tháng 11 2017
Gọi x , y , z lần lượt là độ dài các cạnh của tam giác (cm) ( x , y , z > 0 )
Chu vi của tam giác là 36 cm nên x + y + z = 36
Vì các cạnh của tam giác tỉ lệ với các số 3 , 4 , 5 nên x/3 =y/4 = z/5
Theo tính chất dãy tỉ số bằng nhau ta có :
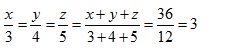
Suy ra : x = 3 . 3 = 9 (TM)
y = 4 . 3 = 12 (TM)
z = 5 . 3 = 15 (TM)
Vậy độ dài các cạnh của tam giác lần lượt là : 9cm , 12cm , 15cm .
a.
Gọi 3 cạnh của tam giác lần lượt là a, b, c.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)
\(\frac{a}{3}=3\Rightarrow a=3\times3=9\)
\(\frac{b}{4}=3\Rightarrow b=3\times4=12\)
\(\frac{c}{5}=3\Rightarrow c=3\times5=15\)
Vậy 3 cạnh của tam giác lần lượt là \(9;12;15\)
b.
Gọi 3 số đó lần lượt là a, b, c.
Áp dụng tính chất của dãy tỉ số băng nhau, ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{480}{10}=48\)
\(\frac{a}{2}=48\Rightarrow a=48\times2=96\)
\(\frac{b}{3}=48\Rightarrow b=48\times3=144\)
\(\frac{c}{5}=48\Rightarrow c=48\times5=240\)
Vậy 3 số đó lần lượt là \(96;144;240\)
Chúc bạn học tốt
Cảm ơn nhiều nhé