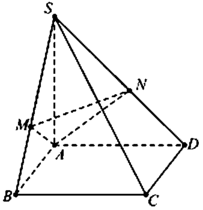
Cho hình chóp SABCD có ABCD là hình vuông cạnh a, SA vuông góc với ABCD. Góc giữa SB ,(ABCD) = 60. Gọi M,N lần lượt là trung điểm của SB,SD. Tính khoảng cách giữa hai đường thẳng AN và CM?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\) (1)
Tam giác SAB vuông cân tại A (do SA=SB=a)
\(\Rightarrow AM\perp SB\) (trung tuyến đồng thời là đường cao) (2)
(1);(2)\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\)
\(\Rightarrow SC\perp\left(AMN\right)\Rightarrow\left(SAC\right)\perp\left(AMN\right)\)
Từ A kẻ \(AH\perp SC\Rightarrow H\in\left(AMN\right)\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{HAC}\) là góc giữa (AMN) và (ABCD)
\(AC=a\sqrt{2}\) ; \(SC=a\sqrt{3}\)
\(sin\widehat{HAC}=cos\widehat{SCA}=\dfrac{AC}{SC}=\sqrt{\dfrac{2}{3}}\Rightarrow\widehat{HAC}\approx54^044'\)

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SMA}\) là góc giữa SM và đáy
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\sqrt{3a^2+\left(\dfrac{2a}{2}\right)^2}.\sqrt{3}=2a\sqrt{3}\)
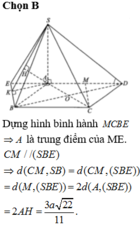
Qua B kẻ đường thẳng song song AM cắt AD kéo dài tại E
\(\Rightarrow AM||\left(SBE\right)\Rightarrow d\left(AM;SB\right)=d\left(AM;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Từ A kẻ \(AH\perp BE\) , từ A kẻ \(AK\perp SH\Rightarrow AK=d\left(A;\left(SBE\right)\right)\)
\(\widehat{DAM}=\widehat{AEB}\) (đồng vị) , mà \(\widehat{BAH}=\widehat{AEB}\) (cùng phụ \(\widehat{ABH}\))
\(\Rightarrow\widehat{DAM}=\widehat{BAH}\)
\(\Rightarrow AH=AB.cos\widehat{BAH}=AB.cos\widehat{DAM}=\dfrac{AB.AD}{AM}=\dfrac{2a.a\sqrt{3}}{2a}=a\sqrt{3}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{3a^2}+\dfrac{1}{12a^2}=\dfrac{5}{12a^2}\)
\(\Rightarrow AK=\dfrac{2a\sqrt{15}}{5}\)

Chọn A
Phương pháp tọa độ (cách này tính toán khá phức tạp nên chỉ nêu ra để học sinh thấy không phải bài toán nào cũng dùng phương pháp tọa độ cũng nhanh nhất)
Ta chọn hệ trục tọa độ như hình vẽ và chọn a = 1.
Ta có:
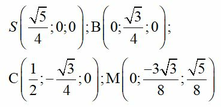
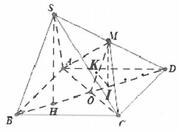

Đáp án là D
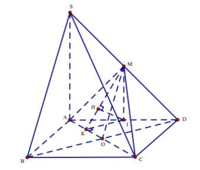
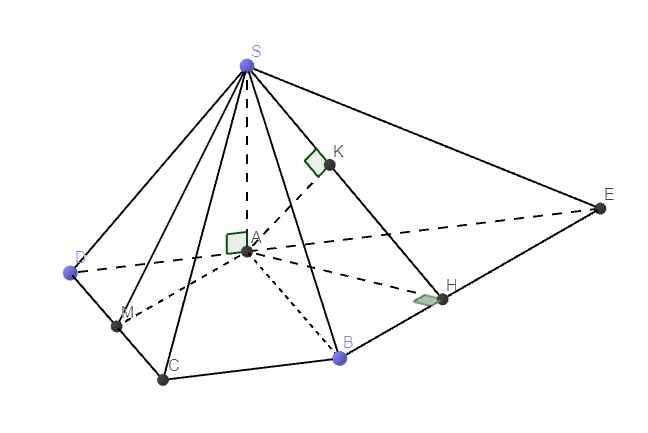
+ Gọi O là giao điểm của AC,BD
⇒ MO \\ SB ⇒ SB \\ ACM
⇒ d SB,ACM = d B,ACM = d D,ACM .
+ Gọi I là trung điểm của AD ,
M I \ \ S A ⇒ M I ⊥ A B C D d D , A C M = 2 d I , A C M .
+ Trong ABCD: IK ⊥ AC (với K ∈ AC ).
+ Trong MIK: IH ⊥ MK (với H ∈ MK ) (1) .
+ Ta có: AC ⊥ MI ,AC ⊥ IK ⇒ AC ⊥ MIK
⇒ AC ⊥ IH (2) .
Từ 1 và 2 suy ra
IH ⊥ ACM ⇒ d I ,ACM = IH .
+ Tính IH ?
- Trong tam giác vuông MIK. : I H = I M . I K I M 2 + I K 2 .
- Mặt khác: M I = S A 2 = a , I K = O D 2 = B D 4 = a 2 4
⇒ I H = a a 2 4 a 2 + a 2 8 = a 3
Vậy d S B , A C M = 2 a 3 .
Lời giải khác
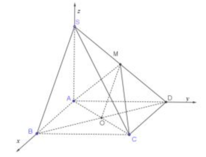


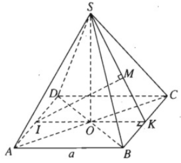
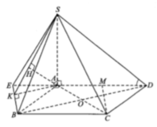
a) Gọi O là tâm hình vuông ABCD , dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên SK ⊥ BC.
Ta có 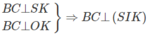
Do đó (SBC) ⊥ (SIK)
b) Hai đường thẳng AD và SB chéo nhau. Ta có mặt phẳng (SBC) chứa SB và song song với AD. Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).
Theo câu a) ta có (SIK) ⊥ (SBC) theo giao tuyến SK và khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK. Dựa vào hệ thức IM. SK = SO. IK
ta có 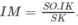
Ta lại có:
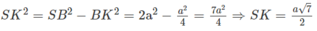
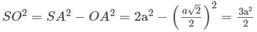
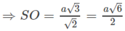
Do đó:
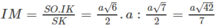
Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng 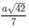

Đáp án B
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .

Từ M kẻ MI//CN =>d(CN,MI)= d(C;SAD)= CD. Yếu tố góc 60 mình không biết có phải thừa hay ko?
bài mình được chữa đây. mn ai thích thì tham khảo nhé. Hay và khó ạ!