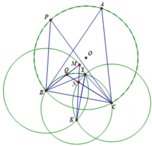
Cho tam giác ABC, P là điểm bất kì trên BC. I, I1, I2 là tâm đường tròn nội tiếp tam giác ABC, APB, APC. Hạ ID vuông góc BC. Chứng minh rằng I1, I2, P, D cùng thuộc một đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi BC tiếp xúc với (I), (I1), (I2) lần lượt tại D,M,N. AP cắt EF tại H và tiếp xúc với (I1),(I2) lần lượt tại Q,R.
Ta có \(EF=MN;EF=HE+HF=2HQ+QR;MN=PM+PN=2PR+RQ\)
Suy ra \(HE=PN\)
Lại có \(DN=PD+PN=CD-CP+PN=\frac{CA+BC-AB+CP+PA-CA-2CP}{2}\)
\(=\frac{BP+PA-AB}{2}=PM\) hay \(PN=DM\). Suy ra \(HE=DM\)
Mà tứ giác EFNM là hình thang cân nên \(HD||EM||FN\)
Nếu gọi DH cắt lại (I) tại K thì các tam giác cân \(EI_1M,KID,FI_2N\) đồng dạng có các cạnh tương ứng song song đôi một
Do đó \(II_1,DM,KE\) đồng quy tại B, \(II_2,DN,KF\) đồng quy tại C
Nói cách khác, BE và CF cắt nhau tại K. Vậy BE và CF gặp nhau trên (I).

1) Ta có
B I C ^ = 180 0 − I B C ^ − I C B ^ = 180 0 − A B C ^ 2 − A C B ^ 2 = 180 0 − 180 ∘ − B A C ^ 2 = 90 0 + B A C ^ 2 ⇔ B A C ^ = 2 B I C ^ − 180 °
Tương tự B Q C ^ = 90 0 + B P C ^ 2 ⇔ B P C ^ = 2 B Q C ^ − 180 ° .
Tứ giác BPAC nội tiếp, suy ra B A C ^ = B P C ^ ⇒ B Q C ^ = B I C ^ , nên 4 điểm B, I, Q, C thuộc một đường tròn.
2) Gọi đường tròn (B; BI) giao (C; CI) tại K khác I thì K cố định.
Góc I B M ^ là góc ở tâm chắn cung I M ⏜ và I K M ^ là góc nội tiếp chắn cung I M ⏜ , suy ra I K M ^ = 1 2 I B M ^ (1).
Tương tự I K N ^ = 1 2 I C N ^ (2).
Theo câu 1) B, I, Q, C thuộc một đường tròn, suy ra I B M ^ = I B Q ^ = I C Q ^ = I C N ^ (3).
Từ (1), (2) và (3), suy ra I K M ^ = I K N ^ ⇒ K M ≡ K N .
Vậy MN đi qua K cố định.

Chú ý góc APC = góc AMC ( t/c đối xứng)
Mà góc AMC = Góc ABC
Chú ý : CH vuông góc AB
Từ đây có ngay kết quả nhe
Gọi \(D'\) là điểm liên hợp đẳng giác với \(A\) trong \(\Delta II_1I_2\), \(IB\) giao \(DE\) tại \(G\)
Ta có \(\widehat{BGD}=\widehat{CDE}-\widehat{DBG}=90^0-\widehat{\frac{1}{2}ACB}-\frac{1}{2}\widehat{ABC}=\frac{1}{2}\widehat{BAC}=\widehat{IAE}\)
Suy ra \(\left(A,F,I,E,G\right)_{cyc}\) hay \(\widehat{IGA}=90^0\)
Vì \(\widehat{D'I_1I_2}=\widehat{GI_1A}\) và \(\widehat{I_1D'I_2}=180^0-\widehat{II_1A}-\widehat{II_2A}=180^0-\left(\widehat{BIC}-\frac{1}{2}\widehat{BAC}\right)=90^0\)
nên \(\Delta I_1GA~\Delta I_1D'I_2\), dẫn đến \(\Delta I_1D'G~\Delta I_1I_2A\)
Suy ra \(\widehat{I_1GD'}=\widehat{I_1AI_2}=\widehat{IAE}=180^0-\widehat{IGE}\), do đó \(\overline{E,G,D'}\) hay \(D'\in DE\)
Tương tự ta có \(D'\in DF\). Từ đó \(D\equiv D'\), suy ra \(\widehat{I_1DI_2}=\widehat{I_1D'I_2}=90^0=\widehat{I_1PI_2}\)
Vậy \(\left(I_1,I_2,P,D\right)_{cyc}.\)