Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn kết hợp S1, S2 cach nhau 8cm dao động cùng pha, sóng sinh ra có bước sóng 1.5cm. N là một điểm thuộc đường trung trực của đoạn thẳng S1 S2 dao động ngược pha với hai nguồn. Khoảng cách nhỏ nhất từ N đến đoạn thẳng S1S2 là
A. 3.4cm
B. 4.2cm
C. 2.6cm
D. 1.8 cm
Lấy giá trị gần đúng nha mọi người. Thanks

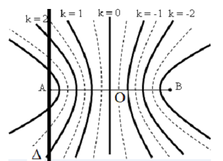
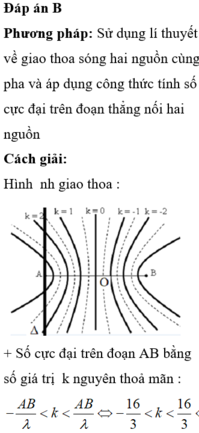

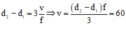
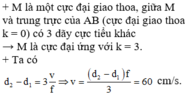




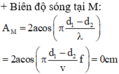
Điểm $N$ dao dộng ngược pha với nguồn nằm trên trung trực của $S_{1}S_{2}$ luôn có khoảng cách đến 2 nguồn là $d=(k-\dfrac{1}{2})\lambda$.
Để $N$ gần $S_{1}S_{2}$ nhất thì $k$ min thỏa mãn $d > 4cm=S_{1}S_{2}:2$ hay $k=4$.
Khi đó khoảng cách cần tìm $=\sqrt{d^2-4^2}=\sqrt{5,25^2-4^2}=3,4cm$