giúp em vẽ hình bài này ạ; Điểm L ở đâu ra vậy ạ? Đây là đề chuyên Trần Phú- Hải Phòng đấy ạ
Cho tứ giác ABCD nội tiếp đường tròn O. Hai tia BA và CD cắt nhau tại K. Hai tia AD và BC cắt nhau tại I. Gọi M,N lần lượt là trung điểm AC và BD. Các đường phân giác trong của các góc BKC và góc BLA cắt nhau tại I. Chứng minh:
a) DKLˆ+DLKˆ=ABCˆ và KILˆ=90∘
b) KM.BD=KN.AC và LM.BD=LN.AC
c) Các đường phân giác trong của góc BKC, góc BLA và đường thẳng MN đồng quy

 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ







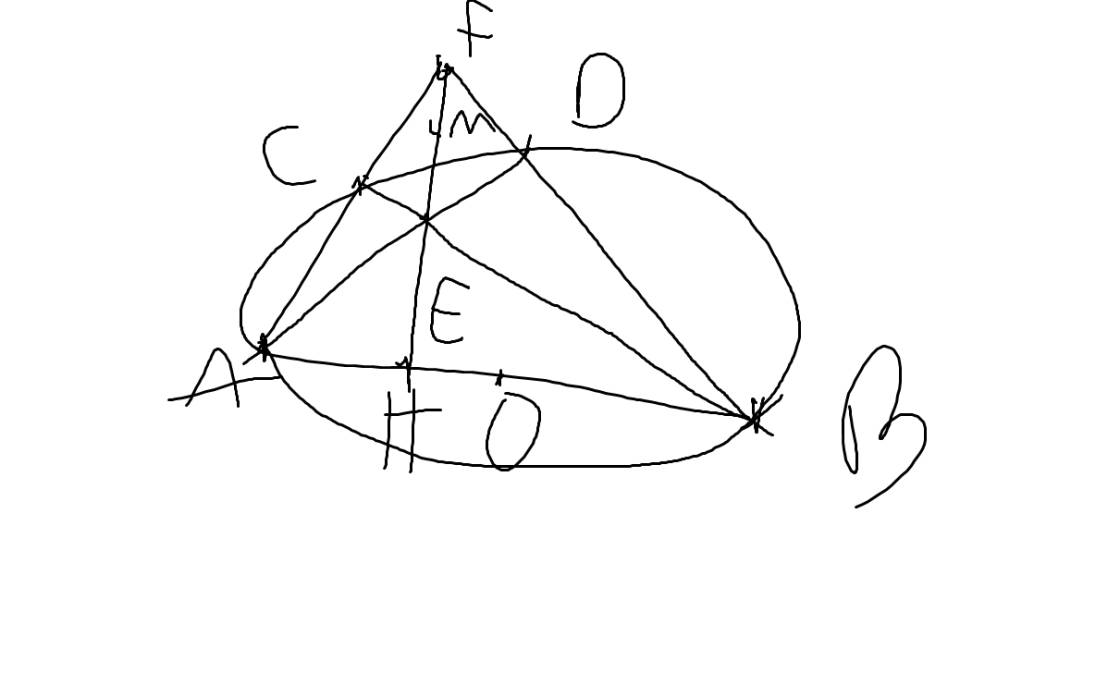



Trong bài này "giả thiết tia AD,BC cắt nhau ở điểm L".
a) Theo tính chất góc ngoài tam giác và góc ngoài của tứ giác nội tiếp ABCD, ta có \(\angle DKL+\angle DLK=\angle LDC=\angle ABC\).
Lại có, \(\angle BKC+\angle BLA=\angle BAD-\angle ADK+\angle BCD-\angle CDL=180^{\circ}-2\angle ADK\)
\(\to\angle IKC+\angle ILD=90^{\circ}-\angle ADK\to\angle IKL+\angle ILK=90^{\circ}-\angle ADK+\angle ABC=90^{\circ}.\)
b) Xét hai tam giác KCA và KBD có góc K chung và \(\angle KCA=\angle KBD\) (cùng chắn 1 cung). Suy ra \(\Delta KCA\sim\Delta KBD\left(g.g\right)\to\frac{KC}{KB}=\frac{CA}{BD}=\frac{CM}{BN}\to\Delta KCM\sim\Delta KBN\left(c.g.c\right)\), do vậy mà \(\frac{KM}{KN}=\frac{CM}{BN}=\frac{AC}{BD}\) . Tương tự ta cũng chứng minh được \(\frac{LM}{LN}=\frac{AC}{BD}.\)
c) Do chứng minh trên \(\angle MKC=\angle NKB\to IK\) cũng là tia phân giác của góc \(\angle MKN\). Tương tự \(LI\) là đường phân giác của góc \(\angle MLN\). Gọi \(J=MN\cap\)phân giác góc \(\angle MKN\). Suy ra \(\frac{JM}{JN}=\frac{KM}{KN}=\frac{LM}{LN}\to LJ\) cũng là phân giác của góc \(\angle MLN\). Vậy \(J\equiv I\), do đó ba đường thẳng: phân giác góc BKC, phân giác BLA và MN đồng quy ở I. (ĐPCM)