Bài 1: Cho tam giác ABC vuông tại A. Đường phân giác của góc B cắt AC tại D. Từ D kẻ DE vuông góc với BC ![]() . Đường thẳng ED cắt BA tại F.
. Đường thẳng ED cắt BA tại F.
a/. Chứng minh▲BDA=▲BDE. Từ đó suy ra ![]() ?
?
b/. Chứng minh BD là đường trung trực của AE
c/. Chứng minh BD vuông góc với CF.

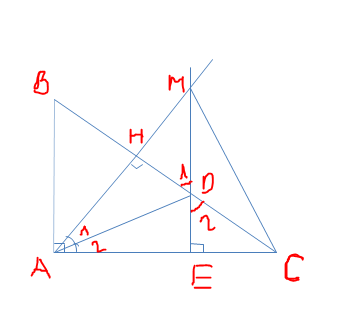


a) Xét ΔBDA vuông tại A và ΔBDE vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác)
Do đó: ΔBDA=ΔBDE(cạnh huyền-góc nhọn)
b) Ta có: ΔBDA=ΔBDE(cmt)
nên BA=BE(hai cạnh tương ứng) và DA=DE(Hai cạnh tương ứng)
Ta có: BA=BE(cmt)
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE