viết phương trình mặt phẳng đi qua điểm N(-3;1;2) và chứa trục Oz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
8 tháng 3 2018
Mặt phẳng đi qua điểm M(1; -2; 4) và nhận n → = (2; 3; 5) làm vectơ pháp tuyến là:
2(x – 1) + 3(y + 2) + 5(z – 4) = 0
⇔ 2x + 3y + 5z – 16 = 0.
27 tháng 3 2023
vecto MN=(1;2)
=>VTPT là (-2;1)
Phương trình MN là:
-2(x-3)+1(y+1)=0
=>-2x+6+y+1=0
=>-2x+y+7=0
Phương trình tham số là:
x=3+t và y=-1+2t
12 tháng 12 2021
a: Vì (d) có hệ số góc là -3 nên a=-3
Vậy: (d): y=-3x+b
Thay x=-1 và y=2 vào (d), ta được:
b+3=2
hay b=-1
CM
8 tháng 2 2019
Hai vecto có giá song song hoặc nằm trên ( α ) là: MN → = (3; 2; 1) và MP → = (4; 1; 0).
Suy ra ( α ) có vecto pháp tuyến là n → = MN → ∧ MP → = (−1; 4; −5)
Vậy phương trình của ( α ) là: -1(x – 1) + 4(y – 1) – 5(z – 1) = 0 hay x – 4y + 5z – 2 = 0
A
Admin
Giáo viên
6 tháng 5 2016
viết phương trình mặt phẳng đi qua M(3;4;-5) và có cặp vectơ chỉ phưowng trình u⃗ =(3;1;−1),v⃗ =(1;−2;1)
\(\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(\left|\begin{matrix}1&-2\\-1&-1\end{matrix}\right|;\left|\begin{matrix}-2&1\\-1&2\end{matrix}\right|;\left|\begin{matrix}1&1\\2&-1\end{matrix}\right|\right)=-3\left(1;1;1\right)\)
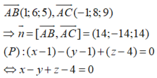
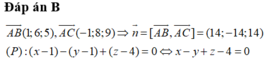
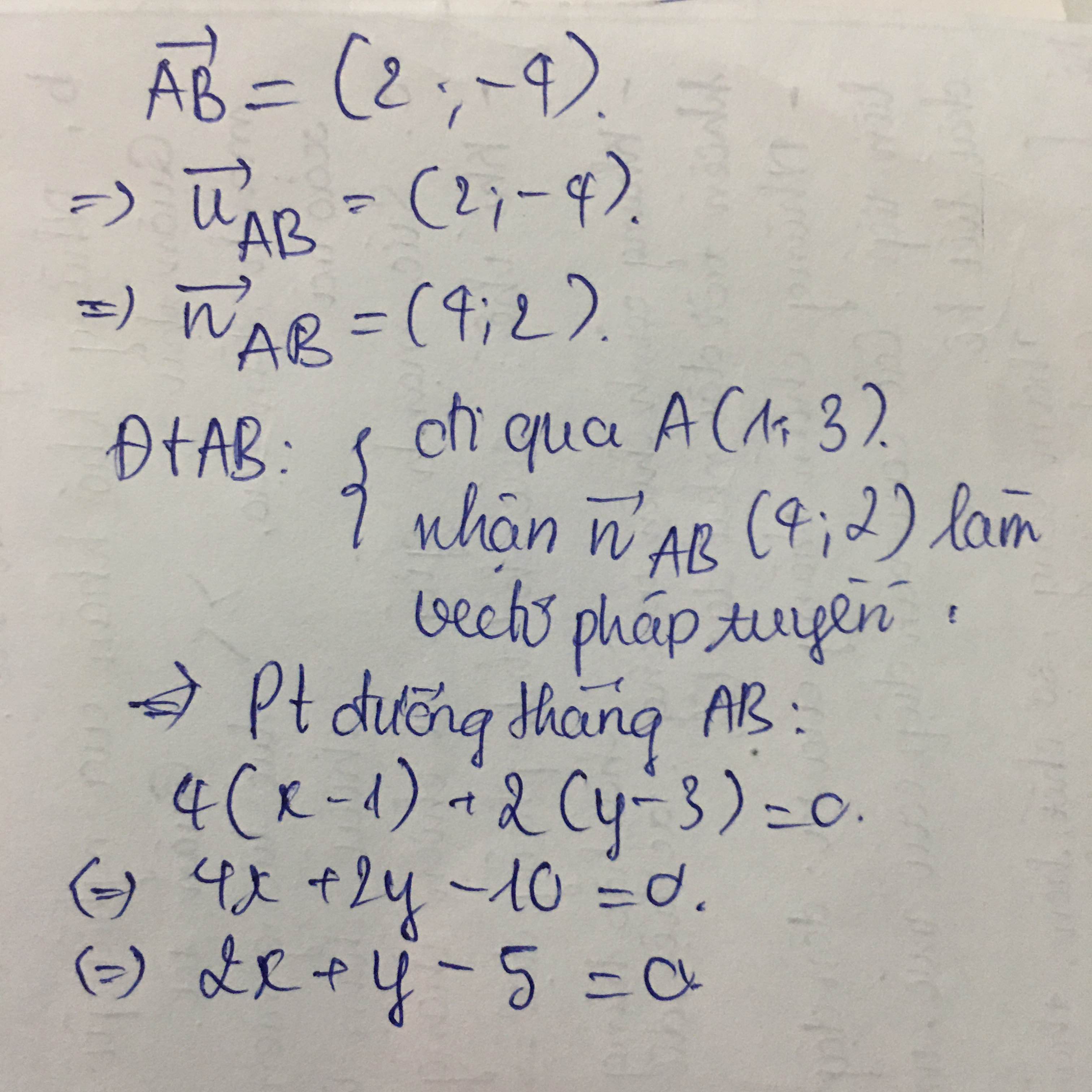
x+3y=0