Dùng định nghĩa tìm các giới hạn sau:
a) ;
b) .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\mathop {\lim }\limits_{x \to - 3} {x^2};\)
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \(\lim {x_n} = - 3.\)
Ta có \(\lim x_n^2 = {\left( { - 3} \right)^2} = 9\)
Vậy \(\mathop {\lim }\limits_{x \to - 3} {x^2} = 9.\)
b) \(\mathop {\lim }\limits_{x \to 5} \frac{{{x^2} - 25}}{{x - 5}}.\)
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \(\lim {x_n} = 5.\)
Ta có \(\lim \frac{{{x_n}^2 - 25}}{{{x_n} - 5}} = \lim \frac{{\left( {{x_n} - 5} \right)\left( {{x_n} + 5} \right)}}{{{x_n} - 5}} = \lim \left( {{x_n} + 5} \right) = \lim {x_n} + 5 = 5 + 5 = 10\)
Vậy \(\mathop {\lim }\limits_{x \to 5} \frac{{{x^2} - 25}}{{x - 5}} = 10.\)

a) Hàm số f(x) = xác định trên R\{
} và ta có x = 4 ∈ (
;+∞).
Giả sử (xn) là dãy số bất kì và xn ∈ (;+∞); xn ≠ 4 và xn → 4 khi n → +∞.
Ta có lim f(xn) = lim =
=
.
Vậy
=
.
b) Hàm số f(x) = xác định trên R.
Giả sử (xn) là dãy số bất kì và xn → +∞ khi n → +∞.
Ta có lim f(xn) = lim = lim
= -5.
Vậy
= -5.

a) Đặt \({u_n} = 2 + {\left( {\frac{2}{3}} \right)^n} \Leftrightarrow {u_n} - 2 = {\left( {\frac{2}{3}} \right)^n}\).
Suy ra \(\lim \left( {{u_n} - 2} \right) = \lim {\left( {\frac{2}{3}} \right)^n} = 0\)
Theo định nghĩa, ta có \(\lim {u_n} = 2\). Vậy \(\lim \left( {2 + {{\left( {\frac{2}{3}} \right)}^n}} \right) = 2\)
b) Đặt \({u_n} = \frac{{1 - 4n}}{n} = \frac{1}{n} - 4 \Leftrightarrow {u_n} - \left( { - 4} \right) = \frac{1}{n}\).
Suy ra \(\lim \left( {{u_n} - \left( { - 4} \right)} \right) = \lim \frac{1}{n} = 0\).
Theo định nghĩa, ta có \(\lim {u_n} = - 4\). Vậy \(\lim \left( {\frac{{1 - 4n}}{n}} \right) = - 4\)
a) Hàm số f(x) = xác định trên R\{
xác định trên R\{ } và ta có x = 4 ∈ (
} và ta có x = 4 ∈ ( ;+∞).
;+∞).
Giả sử (xn) là dãy số bất kì và xn ∈ ( ;+∞); xn ≠ 4 và xn → 4 khi n → +∞.
;+∞); xn ≠ 4 và xn → 4 khi n → +∞.
Ta có lim f(xn) = lim =
=  =
=  .
.
Vậy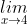
 =
=  .
.
b) Hàm số f(x) = xác định trên R.
xác định trên R.
Giả sử (xn) là dãy số bất kì và xn → +∞ khi n → +∞.
Ta có lim f(xn) = lim = lim
= lim  = -5.
= -5.
Vậy
 = -5.
= -5.