Đề thi học kỳ hai môn văn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 12 2019
Đáp án C
Không gian mẫu là cách chọn môn tự chọn và số mã đề thi có thể nhận được của An và Bình.
• An có C 3 2 cách chọn hai môn tự chọn, có C 8 1 . C 8 1 mã đề thi cỏ thể nhận cho 2 môn tự chọn của An.
• Bình giống An. Nên số phần tử của không gian mẫu là n Ω = C 3 2 . C 8 1 . C 8 1 =36864.
Gọi X là biến cổ “ An và Bình có chung đúng một môn thi tự chọn và chung một mã đề”
Số cách chọn môn thi tự chọn của An và Bình là C 3 1 . 2 ! = 6 .
Trong mồi cặp để mà đề cùa An và Bình giống nhau khi An và Bình cùng mã đề của môn chung, với mỗi cặp có cách nhận mã đề cua An và Bình là C 3 2 . C 8 1 . C 8 1 = 512
Do đó, số kết quả thuận lợi của biến cố X là n X = 6 . 512 = 3072 .
Vây xác suât cân tính là P = n X n Ω = 3072 36864 = 1 12 .
NA
4
21 tháng 4 2021
Đề 1 :
Viết đoạn văn (khoảng 3 - 5 câu ) kể về nghề nghiệp của bố (hoặc mẹ) em theo gợi ý sau:
-
đề 2 :Viết đoạn văn từ 3 đến 5 câu tả về một loài cá mà em biết.
CM
20 tháng 9 2018
Đáp án D
Không gian mẫu là: Ω = 6 4
TH1: Môn Toán trùng mã đề thi môn Tiếng Anh không trùng có:
Bạn Hùng chọn 1 mã toán có 6 cách và 6 cách chọn mã môn Tiếng Anh khi đó Vương có 1 cách là phải giống Hùng mã Toán và 5 cách chọn mã Tiếng Anh có 6.1.6.5 = 180 cách.
TH2: Môn Tiếng Anh trùng mã đề thi môn Toán không trùng có: 6.1.6.5 = 180 cách.
Vậy P = 180 + 180 6 4 = 5 18
CM
6 tháng 9 2017
Đáp án D
Không gian mẫu là: Ω = 6 4
TH1: Môn Toán trùng mã đề thi môn Tiếng Anh không trùng có:
Bạn Hùng chọn 1 mã toán có 6 cách và 6 cách chọn mã môn Tiếng Anh khi đó Vương có 1 cách là phải giống Hùng mã Toán và 5 cách chọn mã Tiếng Anh có 6.1.6.5 = 180 cách.
TH2: Môn Tiếng Anh trùng mã đề thi môn Toán không trùng có: 6.1.6.5 = 180 cách.
Vậy P = 180 + 180 6 4 = 5 18 .
CM
18 tháng 5 2017
Đáp án D
Một bạn học sinh làm 2 môn sẽ có 36 cách chọn đề, do đó 
Hai bạn Hùng và Vương có chung một mã đề thi thì cùng mã toán hoặc cùng mã tiếng anh do đó 
Vậy xác suất cần tính là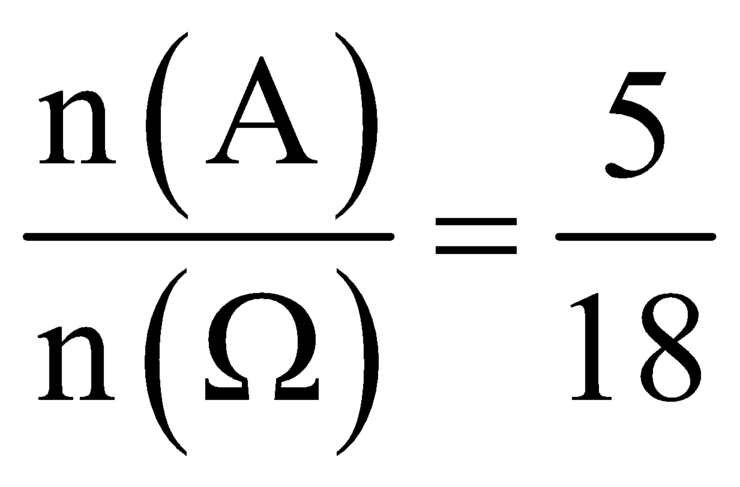 
CM
12 tháng 7 2019
Gọi số học sinh đạt giải cả 3 môn là a (học sinh)
Gọi số học sinh đạt giải cả 2 môn là b (học sinh)
Gọi số học sinh chỉ đạt giải 1 môn là c (học sinh)
Tổng số giải đạt được là: 3 x a + 2 x b + c = 15 (giải).
Vì tổng số học sinh đạt 3 giải, 2 giải, 1 giải tăng dần nên a < b < c.
Vì bất kỳ 2 môn nào cũng có ít nhất 1 học sinh đạt giải cả 2 môn nên:
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Toán.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Toán và Ngoại Ngữ.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Ngoại Ngữ.
Do vậy b= 3.
Giả sử a = 2 thì b bé nhất là 3, c bé nhất là 4; do đó tổng số giải bé nhất là:
3 x 2 + 2 x 3 + 4 = 16 > 15 (loại). Do đó a < 2, nên a = 1.
Ta có: 3 x 1 + 2 x b + c = 15 suy ra: 2 x b + c = 12.
Nếu b = 3 thì c = 12 - 2 x 3 = 6 (đúng).
Nếu b = 4 thì c = 12 - 2 x 4 = 4 (loại vì trái với điều kiện b < c)
Vậy có 1 bạn đạt 3 giải, 3 bạn đạt 2 giải, 6 bạn đạt 1 giải.
Đội tuyển đó có số học sinh là: 1 + 3 + 6 = 10 (bạn).
Câu 1: Đoạn văn trên trích trong văn bản "Dế Mèn phiêu lưu kí". Tác giả là Tôi Hoài. Đoạn văn sử dụng ngôi kể thứ nhất. Dấu hiệu là nhận biết là dế Mèn giới thiệu bản thân bằng chủ ngữ là "tôi".
Câu 2:
-Những ngọn cỏ gãy rạp, y như có một nhát dao vừa lia qua.
Phép so sánh ấy thuộc kiểu so sánh ngang bằng.
Tối quá!!!!!!! Dù sao mk cũng cảm lưn bạn, mai mình thi rùi