Tìm đạo hàm các hàm số sau:
y = x3 - 2x + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 9 2021
a.
\(y'=4x^3+8x=4x\left(x^2+2\right)=0\Rightarrow x=0\)
Dấu của y':
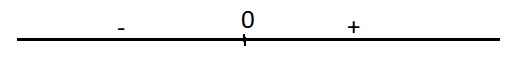
Hàm đồng biến trên \(\left(0;+\infty\right)\) và nghịch biến trên \(\left(-\infty;0\right)\)
b.
\(y'=3x^2+6x+3=3\left(x+1\right)^2\ge0\) ; \(\forall x\)
\(\Rightarrow\) Hàm đồng biến trên R
21 tháng 6 2023
\(y'=\dfrac{1}{5}\cdot5x^4+\dfrac{1}{2\sqrt{x}}+\dfrac{1}{x^2}+\dfrac{-\left(x^3\right)'}{x^6}\)
\(=x^4+\dfrac{1}{2\sqrt{x}}+\dfrac{1}{x^2}+\dfrac{-3x^2}{x^6}=x^4+\dfrac{1}{2\sqrt{x}}+\dfrac{1}{x^2}-\dfrac{3}{x^4}\)
PT
1
N
1
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 2 2021
\(g\left(x\right)=f\left(1-2018x\right)\Rightarrow g'\left(x\right)=-2018f'\left(1-2018x\right)\)
\(\Rightarrow\) Số nghiệm của \(g'\left(x\right)\) bằng số nghiệm \(f'\left(x\right)\Rightarrow g'\left(x\right)\) có 4 nghiệm
\(g\left(x\right)=0\Leftrightarrow f\left(1-2018x\right)=0\) có số nghiệm bằng số nghiệm f(x)
Do \(f'\left(x\right)\) có 4 nghiệm nên f(x) có tối đa 5 nghiệm
Vậy hàm có tối đa 9 cực trị
CM
26 tháng 2 2017
Chọn A.
Ta có: f’(x) = 3x2 – 6x.
f’(x) < 0 ⇔ 3x2 – 6x < 0 ⇔ 0 < x < 2.
y'= \(3x^2\)-2