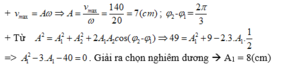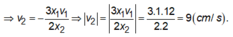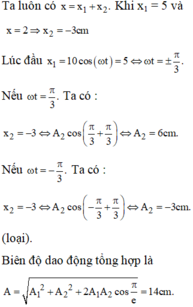Một chất điểm tham gia đồng thời 2 dao động điều hòa cùng phương, cùng vị trí cân bằng, với phương trình li độ x1=A1cos(2pit+pi/6) và x2=8cos(2pit-pi/2).Điều chỉnh A1 cho đến khi biên độ dao động tổng hợp đạt giá trị cực tiểu thì giá trị cực tiểu đó bằng bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
28 tháng 8 2015
1,vật qua vị trí x=-5 => thay x vào phương trình dao động .
2,T=0,4 s=> t=1s=2,5 T=2T+0,5T. 2chu kì sẽ đi qua x=1 bốn lần,thêm một nửa chu kì nữa được 1 lần.tổng cộng là 5 lần. Vẽ đường tròn ra nha cậu
3, denta t= 4,625-1=3,625 s=3,625 T=3T+1/2 T+1/8 T
tại t1=1s,x=căn 2.
quãng đường đi được trong 3,625 T=3. 4A+2A+A căn 2/2 .Vì một ch kì vật đi được 4A,cậu cũng vè đường tròn ra là thấy
S=29,414 cm ,v=S/t= 29,414/3,625=8,11 cm/s.
4.Tự làm nốt nhé,cứ ốp vào dường tròn là ra ngay.
HY
10 tháng 3 2015
Vật thực hiện 2 dao động
\(x_1 = 2 \sin (2\pi t + \frac{\pi}{6}) = 2 \cos (2\pi t + \frac{\pi}{6} - \frac{\pi}{2}) = 2 \cos (2\pi t - \frac{\pi}{3})cm.\)
\(x_2 = A_2\cos (2\pi t + \varphi_2)cm\)
Như vậy vật coi như dao động với dao động tổng hợp là: \(x = A \cos (2\pi t + \varphi)\)
Tại thời điểm \(t = \frac{t}{6}s ; x = \frac{A}{2} = 1cm => A = 2cm.\) :
\(\frac{A}{2} = A \cos (2 \pi .\frac{t}{6} + \varphi)\)
=> \(\cos (\frac{\pi}{3}+ \varphi) = \frac{1}{2}\)
=> \(\frac{\pi}{3} + \varphi = \frac{\pi}{3} => \varphi = 0. \)
hoặc \(\frac{\pi}{3} + \varphi =- \frac{\pi}{3} = > \varphi = \frac{-2\pi}{3}\)
Mà vật chuyển động theo chiểu âm tức là \(v = x' = -A\omega \sin (\frac{\pi}{3} + \varphi) <0\)
=> \(\sin (\omega t + \varphi ) > 0 => \) Chọn \(\varphi = 0.\)
Dựng giản đồ véc tơ
\(\triangle OA_1A\) đều vì \(A= A_1 = 2cm; OA_1A = 60^0\)
=> \(A_2 = A= A_1 = 2cm; \varphi_2 = OAA_1 = \frac{\pi}{3}.\)
Chọn đáp án.A
HD
Hà Đức Thọ
Admin
4 tháng 8 2015
Bài này đơn giản thôi, mình gợi ý thế này nhé.
+ Bạn tìm x2 = x - x1 bằng cách bấm máy tính.
Thay t = 1s vào tính.
VT
23 tháng 10 2019
Đáp án D
+ Hai động động thành phần có độ lệch pha ∆ φ = ( 2 k + 1 ) π → hai dao động ngược pha => biên độ dao động tổng hợp đạt cực tiểu.
