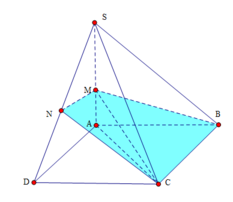
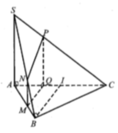
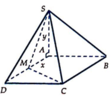
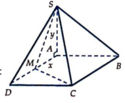
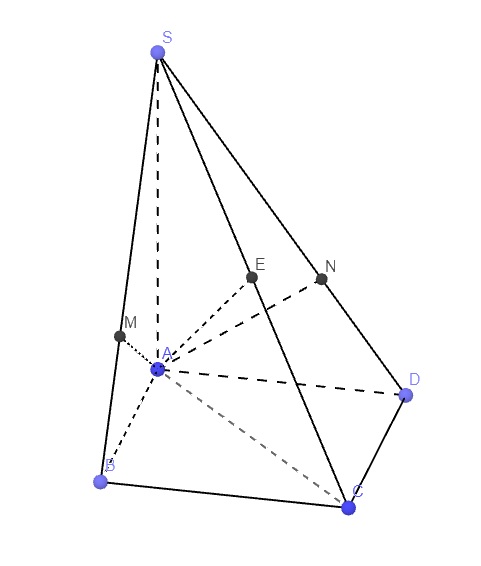
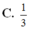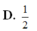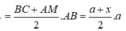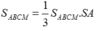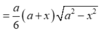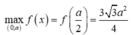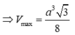cho hình chóp SABCD đáy là hình vuông cạnh a. chiều cao SA=a. M là 1 điểm trên đoạn AC, AM=x (0<x< a căn 2). Gọi (P) là mặt phẳng qua M, song song với BD và vuông góc với mp đáy.
a, xác định và tính diện tích thiết diện của (P) với hình chóp.
b. xác đinh vị trí của M để thiết diện có diện tích lớn nhất .