Cho tứ giác MNPQ sao cho hai đường chéo MP và NQ vuông góc với nhau. Gọi I, K, R, S theo thứ tự là trung điểm của các cạnh MN, NP, PQ, QM.
a) Chứng minh IKRS là hình chữ nhật
b) Điều kiện để IKRS là hình vuông
c) SIKRS biết MP=8cm; NQ=14cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

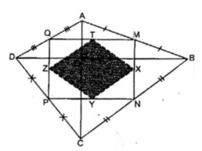
Trong △ ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của △ ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong △ CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của △ CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong △ ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 90 0
Vậy tứ giác MNPQ là hình chữ nhật.

CHẮC LÀ PHẢI CHIM TO PHẢI CHIM TOOOOOOOOOOOOOOOOOOOOOOOOOOOO

a.Ta có MNPQMNPQ là hình bình hành
→MQ//NP,MQ=NP→MQ//NP,MQ=NP
Mà F,EF,E là trung điểm MQ,NPMQ,NP
→MF=FQ=12MQ=12NP=NE=EP→MF=FQ=12MQ=12NP=NE=EP
→FQ=NE→FQ=NE
→NFQE→NFQE là hình bình hành
→NF//QE→QE//NK→NF//QE→QE//NK
→NEQK→NEQK là hình thang
b.Ta có MF//NE,MF=NEMF//NE,MF=NE
→MNEF→MNEF là hình bình hành
Mà NP=2MN→MN=12NP=NENP=2MN→MN=12NP=NE
→MNEF→MNEF là hình thoi
→ME⊥NF,EM→ME⊥NF,EM là phân giác ˆNEFNEF^
Tương tự FP⊥EQ,EQFP⊥EQ,EQ là phân giác ˆFEPFEP^
Lại có ˆNEF+ˆFEP=180o→ME⊥QENEF^+FEP^=180o→ME⊥QE
→GFHE→GFHE là hình chữ nhật
c.Để GFHEGFHE là hình vuông
→FE→FE là phân giác ˆGFHGFH^
→FE→FE là phân giác ˆNFPNFP^
→EF⊥NP→EF⊥NP
→MN⊥NP→MN⊥NP
→MNPQ→MNPQ là hình chữ nhật