Tìm m để hàm số \(y=x^4-2m^2x^2+1\) có 3 điểm cực trị là 3 đỉnh của một tam giác vuông cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
\(y'=4mx^3-8x=0\Rightarrow\left[{}\begin{matrix}x=0\\mx^2=2\end{matrix}\right.\)
Hàm có 3 cực trị khi \(m>0\)
Gọi 3 cực trị là A, B, C với \(\left\{{}\begin{matrix}A\left(0;1\right)\\B\left(\sqrt{\dfrac{2}{m}};1-\dfrac{4}{m}\right)\\C\left(-\sqrt{\dfrac{2}{m}};1-\dfrac{4}{m}\right)\end{matrix}\right.\)
Gọi H là trung điểm BC \(\Rightarrow H\left(0;1-\dfrac{4}{m}\right)\)
\(AH=\left|y_A-y_H\right|=\dfrac{4}{m}\) ; \(BC=\left|x_B-x_C\right|=2\sqrt{\dfrac{2}{m}}\)
Tam giác ABC luôn cân tại A nên nó vuông cân khi \(AH=\dfrac{1}{2}BC\)
\(\Leftrightarrow\dfrac{4}{m}=\sqrt{\dfrac{2}{m}}\Rightarrow m=8\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
\(y'=4x^3-4mx=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=m\end{matrix}\right.\)
Hàm có 3 cực trị khi \(m>0\)
Gọi 3 cực trị là A; B; C với \(\left\{{}\begin{matrix}A\left(0;m^4+2m\right)\\B\left(\sqrt{m};2m\right)\\C\left(-\sqrt{m};2m\right)\end{matrix}\right.\)
Tam giác ABC luôn cân tại A, gọi H là trung điểm BC \(\Rightarrow H\left(0;2m\right)\)
\(AH=\left|y_A-y_H\right|=m^4\) ; \(BC=\left|x_B-x_C\right|=2\sqrt{m}\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.m^4.2\sqrt{m}=4\)
\(\Leftrightarrow m^9=16\Rightarrow m=\sqrt[3]{2}\)
CM
4 tháng 7 2019
Đáp án D
Áp dụng công thức giải nhanh cho tam giác vuông cân (tam giác luôn cân):
22 tháng 11 2016
\(y'=4x\left(x-m\right)\left(x+m\right)\\ y'=0\Leftrightarrow\begin{cases}x=0\\x=\pm m\end{cases}\)
Với m=0 thì hàm số có 3 cực trị là 0, -m và m
đồ thị hàm số có 3 điểm cực trị \(A\left(0;1\right),M\left(-m;1-m^4\right),N\left(m;1-m^4\right)\)
Nhận thấy \(AM=AN\) nên \(\Delta AMN\) cân tại A với mọi m
Gọi trung điểm MN là \(I\left(0;1-m^4\right)\)
\(\Delta AMN\) vuông cân tại A khi và chỉ khi \(IA=IM=IN\) hay\(IA=IN\)
\(\Leftrightarrow IA=IN\Leftrightarrow\left|m^4\right|=\left|m\right|\Leftrightarrow m=\pm1\) (vì \(m\ne0\))
CM
22 tháng 7 2019
Đáp án là B
TXĐ D= ℝ
Cách 1.
Ta có: y ' = 4 x 3 − 4 m x = 4 x x 2 − m
Do hàm số đã cho là hàm số trùng phương nên để đồ thị hàm số y = x 4 − 2 m x 2 + 2 m − 3 có ba điểm cực trị là ba đỉnh của một tam giác cân thì phương trình y ¢= 0 phải có 3 nghiệm thực phân biệt.
Û x 2 = m có hai nghiệm phân biệt x ¹ 0 Û m > 0 .
Cách 2. (Dùng cho trắc nghiệm)
Do hàm số đã cho là hàm số trùng phương nên để đồ thị hàm số y = x 4 − 2 m x 2 + 2 m − 3 có ba điểm cực trị là ba đỉnh của một tam giác cân thì a . b < 0 ⇔ 1. − 2 m < 0 ⇔ m > 0.
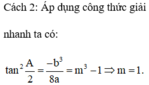
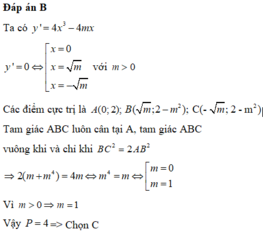
Hàm số xác định trên R
Ta có \(y'=4x^3-4m^2x=4x\left(x^2-m^2\right)\)
Suy ra hàm số có 3 cực trị \(\Leftrightarrow m\ne0\)
Khi đó tọa độ các điểm cực trị của đồ thị hàm số là \(A\left(0;1\right);B\left(m;1-m^4\right);C\left(-m;1-m^4\right)\)
Ta thấy AB = AC nên tam giác ABC vuông cân \(\Leftrightarrow AB^2+AC^2=BC^2\)
\(\Leftrightarrow2\left(m^2+m^8\right)=4m^2\Rightarrow m=\pm1\)
Vậy \(m=\pm1\) là giá trị cần tìm