Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng a, cạnh bên bằng \(\frac{a\sqrt{5}}{2}\). Tính góc tạo bởi mặt bên và mặt đáy, tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 1 2018
Đáp án: D
Hướng dẫn giải:
Gọi O là giao điểm của AC và BD, M là trung điểm của SA.
Qua M kẻ đường thẳng vuông góc với SA cắt SO tại I
⇒ I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD
⇒ S I = R = 2
Ta có:
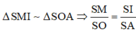
⇒ S O = S M . S A S I = S A 2 2 2
⇒ S A = S O 2
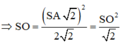
⇒ A B = 2 ⇒ S A B C D = A B 2 = 4
⇒ V S . A B C D = 1 3 . S O . S A B C D = 4 2 3
CM
11 tháng 8 2018
Đáp án C
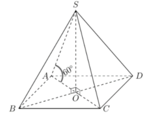
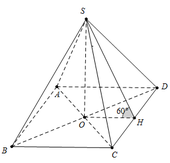
Gọi O là tâm đáy ABCD. Khi đó S O ⊥ A B C D
suy ra AO là hình chiếu vuông góc của SA lên mặt phẳng đáy. Khi đó góc giữa cạnh bên SA và đáy là S A O ^
Suy ra S A O ^ = 60 °
Vậy thể tích khối chóp là:
V = 1 3 . S O . S A B C D = a 3 6 6
CM
8 tháng 8 2019
Đáp án B
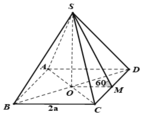
Ta có: 2 B I 2 = a 2 ⇒ B I = a 2 ; S I = B I tan 60 0 = a 3 2
Thể tích khối chóp S.ABCD là
V = 1 3 S I . S A B C D = 1 3 a 3 2 . a 2 = a 3 6 6
CM
18 tháng 9 2019
Đáp án A
Gọi O là tâm hình vuông ABCD, M là trung điểm CD.
Khi đó SO là đường cao hình chóp, góc SMO là góc giữa mặt bên và mặt đáy của hình chóp.
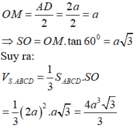
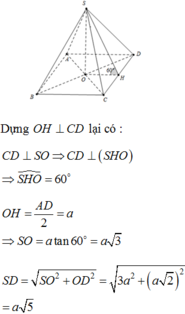
Gọi H là tâm của ABCD\(\Rightarrow SH\perp\left(ABCD\right)\)
M là trung điểm của BC \(\Rightarrow BC\perp\left(SHM\right)\)
Do các mặt bên tạo với đáy cùng 1 góc => \(\widehat{SHM}\) bằng góc tạo bởi 2 mặt bên với đáy
Tính được \(SH=\frac{a\sqrt{3}}{2}'HM=\frac{a}{2}\)
\(\tan\widehat{SMH}=\frac{SH}{MH}=\sqrt{3}\Rightarrow\widehat{SMN}=60^0\)
Lập luận được tâm khối cầu là điểm I của SH với trung trực SC trong (SHC)
Tính được bán kính khối cầu do tam giác SNI đồng dạng với tam giác SHC
\(\Rightarrow SI=\frac{SN.SC}{SH}=\frac{5a}{4\sqrt{3}}\)
Vậy \(V=\frac{4}{3}\pi R^2=\frac{125a^3\sqrt{3}\pi}{432}\)