Có một quả bóng hình cầu đặc đường kính 20cm được đặt đứng yên trên mặt phẳng nằm ngang. Người ta lấy một chiếc nón úp vào quả bóng thì thấy đáy nón vừa chạm với mặt phẳng nằm ngang và các đường sinh của mặt nón cũng vừa tiếp xúc với bề mặt của quả bóng. Biết rằng độ rộng của góc ở đỉnh nón là \(60^0\). Tính thể tích của khối nón giới hạn bởi chiếc nón và mặt phẳng nằm ngang và tính phần không gian bên trong khối nón mà không bị quả bóng chiếm chỗ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
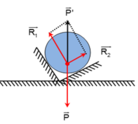
Các lực tác dụng lên quả tạ được biểu diễn như hình
Điều kiện cân bằng của quả tạ là


Chọn A.
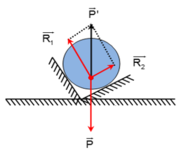
Các lực tác dụng lên quả tạ được biểu diễn như hình
Điều kiện cân bằng của quả tạ là
R 1 ⇀ + R 2 ⇀ = P ' ⇀ = - P ⇀
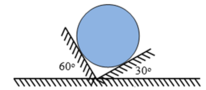
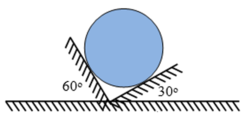
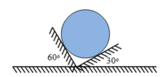
Do 30° + 60° = 90° → = 90°
→ R 1 = Pcos30° = 8.10.cos30° = 40√3 N
→ R 2 = Pcos60° = 8.10.cos60° = 40 N

Chọn D.
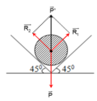
Các lực tác dụng lên quả tạ được biểu diễn như hình.
Điều kiện cân bằng của quả tạ là
![]()
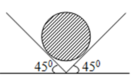
Do hai góc nghiêng đều là 45o nên ta có:
R1 = R2 = P.cos45o = 5.10.cos45o = 25 N.

Chọn D.
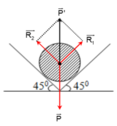
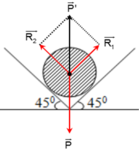
Các lực tác dụng lên quả tạ được biểu diễn như hình.
Điều kiện cân bằng của quả tạ là:
R 1 ⇀ + R 2 ⇀ = P ' ⇀ = - P ⇀
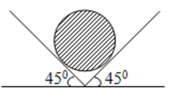
Do hai góc nghiêng đều là 45° nên ta có:
R 1 = R 2 = P.cos45° = 5.10.cos45° = 25√2 N.

Các lực tác dụng lên vật như hình 53.
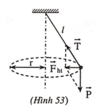
Lực hướng tâm là hợp lực của trọng lực P → và lực căng dây T → . Dùng định luật II Niu-tơn thu được số vòng quay trong một giây:
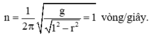





Giả sử căt hình đó thành 1 mặt phẳng đi qua trục của nón ta được thiết diện như hình vẽ. Trong đó tam giác ABC là tam giác đều và là thiết diện của khối nón. Hình tròn tâm I là thiết diện của quả bóng.
Ta nhận thấy tam giác ABC ngoại tiếp đường tròn tâm I
Hình nón có chiều cao là \(OH=3IH=30\) (cm)
Bán kính đáy nón là \(HA=\frac{30}{\sqrt{3}}=10\sqrt{3}\left(cm\right)\)
Thể tích khối nón là \(V_1=\frac{1}{3}OH.\pi.AH^2=\frac{1}{3}.30\pi.300=3000\pi\left(cm^3\right)\)
Thể tích phần không gian bên trong khối nón không bị quả bóng chiếm chỗ là :
\(V_2=\frac{1}{3}OH.\pi.AH^2-\frac{1}{4}\pi.IH^2=3000\pi-\frac{4000}{3}\pi=\frac{5000}{3}\pi\left(cm^3\right)\)