Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh SB, BC, CD. Chứng minh rằng AM vuông góc với BP và tính thể tích của khối tứ diện CMNP
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B.
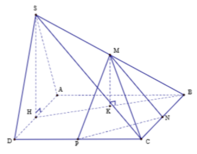
Gọi H là trung điểm của cạnh AD. Do tam giác SAD đều nên SH ⊥ AD
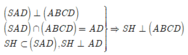
Gọi K là trung điểm của HB => MK//SH
Do đó: MK ⊥ ABCD => MK ⊥ (CNP).
Vậy MK là chiều cao của khối tứ diện CMNP.
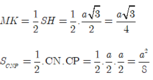
Thể tích khối tứ diện CMNP là
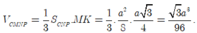

Chọn D.
Áp dụng công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp R 2 = x 2 + r 2 với
r là bán kính đường tròn ngoại tiếp đa giác đáy
x = S O 2 - r 2 2 h : S là đỉnh hình chóp , O là tâm đường tròn ngoại tiếp đa giác đáy, h là chiều cao hình chóp
Cụ thể vào bài toán:
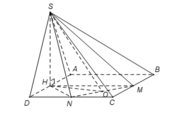
Đáy là tam giác CMN vuông tại C
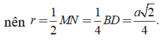
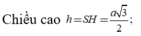
Tâm O của đường tròn ngoại tiếp tam giác CMN là trung điểm MN
Áp dụng công thức đường trung tuyến trong tam giác HMN tính được H O 2 = 5 a 2 8
Trong tam giác vuông SHO có
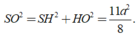
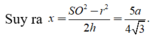
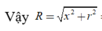
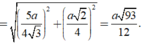

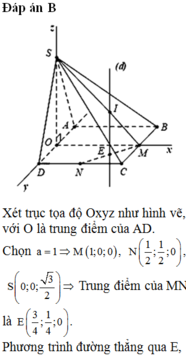
Đáp án B
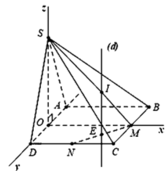
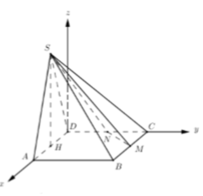
Xét trục tọa độ Oxyz như hình vẽ, với O là trung điểm của AD
Chọn a = 1 => 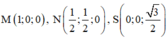 => Trung điểm của MN là
=> Trung điểm của MN là 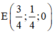
Phương trình đường thẳng qua E, song song với Oz là 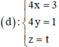
Gọi I là tâm mặt cầu cần tìm => 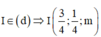
Suy ra 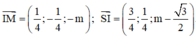
Mà 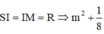
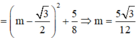
Vậy 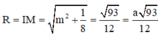

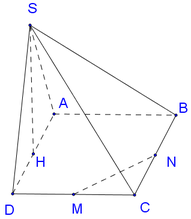
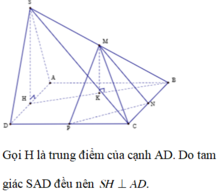




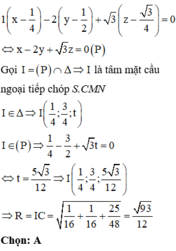

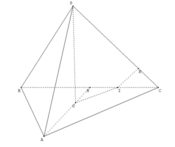

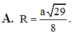
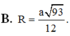
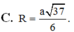
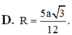

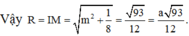
Gọi H là trung điểm của AD. Do tam giác SAD là tam giác đều nên SH vuông góc với AD
Do mặt phẳng (SAD) vuông góc với mặt phẳng (ABCD) nên SH vuông góc với BP(1)
Xét hình vuông ABCD ta có :
\(\Delta CDH=\Delta BCP\Rightarrow CH\perp BP\) (2)
Từ (1) và (2) ta suy ra \(BP\perp\left(SHC\right)\)
Vì \(\begin{cases}MN||SC\\AN||CH\end{cases}\) \(\Rightarrow\left(AMN\right)||\left(SHC\right)\)
\(\Rightarrow BP\perp\left(AMN\right)\Rightarrow BP\perp AM\)
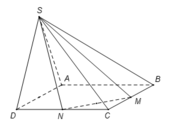
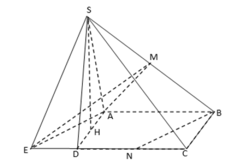
Kẻ vuông góc với mặt phẳng (ABCD), K thuộc vào mặt phẳng (ABCD), ta có :
\(V_{CMNP}=\frac{1}{3}MK.S_{CNP}\)
Vì \(MK=\frac{1}{2}SH=\frac{a\sqrt{3}}{4};S_{CNP}=\frac{1}{2}CN.CP=\frac{a^2}{8}\)
\(\Rightarrow V_{CMNP}=\frac{\sqrt{3}a^2}{96}\)