Chứng minh rằng hàm số y =
#Hỏi cộng đồng OLM
#Mẫu giáo
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TXĐ: D = [0; 2]
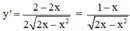
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 0 < x < 1.
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 < x < 2.
Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).

TXĐ: D = R
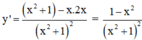
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 – x2 < 0
⇔ x2 > 1
⇔ x ∈ (-∞ ; -1) ∪ (1; +∞).
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 1 – x2 > 0
⇔ x2 < 1
⇔ x ∈ (-1; 1).
Vậy hàm số đồng biến trên khoảng (-1; 1) và nghịch biến trên các khoảng (-∞; -1) và (1; +∞).

Với mọi tham số m ta có :
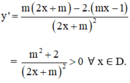
Vậy hàm số luôn đồng biến trên mỗi khoảng xác định của nó.

y = ( a 2 - 2a + 4)x - 9
Ta có: a 2 - 2a + 4 = a 2 - 2a + 1 + 3 = a - 1 2 + 3 > 0 ∀a
Vậy hàm số luôn đồng biến trên R

Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng
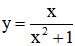
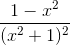 => y' = 0 ⇔ x=-1 hoặc x=1.
=> y' = 0 ⇔ x=-1 hoặc x=1.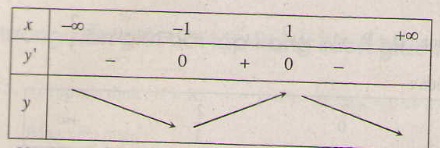
Tập xác định : D = [0 ; 2]; y' = , ∀x ∈ (0 ; 2); y' = 0 ⇔ x = 1.
, ∀x ∈ (0 ; 2); y' = 0 ⇔ x = 1.
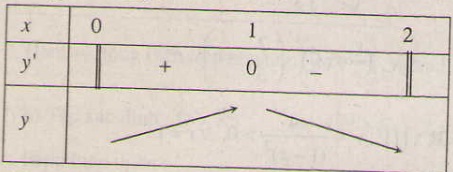
Bảng biến thiên :
Vậy hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên khoảng (1 ; 2).