Cho hình bình hành ABCD, AB=12, AD= 15, ^BAD=110. Tính diện tích ABCD.
tớ cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 1 2019
*Khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = x, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón
Trong tam giác AHD,ta có:
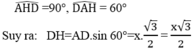
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
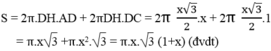
*Khi quay hình bình hành ABCD một vòng quanh AD thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AB = DC = 1, cạnh BC vạch nên hình trụ có bán kính đáy bằng bán kính đáy của hình nón
Ta có:
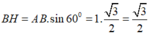
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
NA
1
8 tháng 8 2021
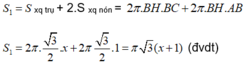
Ta có AB//CD
\(\Rightarrow\widehat{DAB}+\widehat{ADC}=180\\ \Rightarrow\widehat{ADC}+135=180\\ \Rightarrow\widehat{ADC}=45\)
Ta có \(\sin D=\sin45=\dfrac{AH}{AD}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\dfrac{AH}{15}=\dfrac{\sqrt{2}}{2}\left(cm\right)\\ \Rightarrow AH=\dfrac{15\sqrt{2}}{2}\left(cm\right)\\ \Rightarrow S_{ABCD}=AB\cdot AH=18\cdot\dfrac{15\sqrt{2}}{2}=135\left(cm^2\right)\)
KV
4 tháng 11 2023
Chu vi hình bình hành ABCD:
(AB + AD) . 2 = 90 (cm)
AB + AD = 90 : 2 = 45 (cm)
\(2x+x=45\left(cm\right)\)
\(3x=45\left(cm\right)\)
\(x=45:3=15\left(cm\right)\)
\(\Rightarrow AB=2.15=30cm;AD=15cm\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
5 tháng 5 2022
Ta có CF=DE=CD=4 cm
=> BC=AD=32:2-4=12 cm
Hình thoi CDEF và hình bình hành ABCD có chung đường cao từ C->AE nên
\(\dfrac{S_{CDEF}}{S_{ABCD}}=\dfrac{DE}{AD}=\dfrac{4}{12}=\dfrac{1}{3}\Rightarrow S_{ABCD}=3.S_{CDEF}=3.54=162cm^2\)
CM
28 tháng 10 2018
Kẻ DH ^ AB tại H
⇒ A H = A D 2 = 4 c m
Áp dụng định lý Pytago trong D vuông ADH Þ DH = 4 3 cm.
ÞSABCD = DH.AB = 120cm2
Do ABCD là hình bình hành \(\Rightarrow\widehat{B}=180^0-\widehat{BAD}=70^0\)
Kẻ đường cao AH ứng với BC
Trong tam giác vuông ABH:
\(sinB=\dfrac{AH}{AB}\Rightarrow AH=AB.sinB\)
\(\Rightarrow S_{ABCD}=AH.AD=AB.AD.sinB=12.15.sin70^0\approx169,1\left(cm^2\right)\)